Борьба с COVID-19 в Германии, в России и в Москве. Байесовский вывод и модель SIR. Прогнозы и рассуждения об эффективности тестирования.
Незаметно пролетел второй месяц самоизоляции. Пик эпидемии в нашей стране, вроде как, уже пройден. В результате Россия теперь находится в топ-3 🏆 стран по количеству подтверждённых случаев заболевания COVID-19. Главным очагом эпидемии, разумеется, стал Московский регион, где суммарное число официально заболевших к концу мая превысило 200 тысяч человек — более 50% всех случаев по стране. Разного рода ограничительных мер с переменным успехом тут тоже вводилось больше, чем в других регионах. Именно они и будут одним из основных объектов исследований в этом посте.
Модель SIR 2.0
Количество публикаций по текущей пандемии COVID-19 🦇 просто зашкаливает. Модели распространения, новые прогнозы и различные статистические оценки параметров этого заболевания появляются каждый день. Одной из интересных статей по коронавирусной тематике является работа немецких аспирантов из Института динамики и самоорганизации Общества Макса Планка (Max Planck Institute for Dynamics and Self-Organization, MPIDS) в Гёттингене. Это один из 80 институтов Общества научных исследований имени Макса Планка (Max-Planck-Gesellschaft, MPG), который занимается исследованием сложных неравновесных систем, в частности, в физике и биологии. Статья Inferring change points in the COVID-19 spreading reveals the effectiveness of interventions доступна для ознакомления на arXiv.org. Помимо текста работы, также доступен репозиторий с иходниками, на базе которых осуществлялись расчёты в статье. Точнее два репозитория: первый — с моделями непосредственно из статьи, второй — репозиторий, в котором ведётся активная разработка, и продолжают вводиться разного рода оптимизации (API периодически меняется). В этом посте мы будем использовать последний, и адаптируем эту модель к российским реалиям.
Одной из моделей, рассматриваемых в статье, является известная нам по предыдущему посту модель SIR, которая представляет собой нелинейную систему обыкновенных дифференциальных уравнений (ДУ), описывающих динамику распространения заболевания в популяции:
Здесь $S$, $I$, $R$ — текущее количество восприимчивых (susceptible), инфицированных/заразных (infectious) и переболевших (removed) индивидов соответственно в текущий момент времени $t$, $N$ — размер популяции, в которой распространяется патоген, $\lambda$ — эффективная частота контактов между индивидами (effective contact rate), $\mu$ — коэффициент интенсивности перехода инфицированных индивидов в группу переболевших (интенсивность выбывания, removal rate), обратно пропорциональный времени, в течение которого больной может заражать 🤧 других.
Эта модель достаточна проста и обычно подразумевает, что эффективная частота контактов $\lambda$ и интенсивность выбывания $\mu$ не меняются в течение эпидемии. Предложенная в статье модель SIR является её расширенным вариантом с байесовским выводом основных эпидемиологических параметров на начальном этапе эпидемии (экспоненциального роста заболевших). В ней реализована возможность обнаружения/введения потенциальных точек изменений (change points) эффективной частоты контактов $\lambda$ между индивидами, вызванных введением разного рода ограничительных мер. Будем называть эти точки 📌 контрольными. Таким образом, модель осуществляет оценку эффективной частоты контактов на основе данных о подтверждённых случаях заболевания COVID-19, комбинируя байесовский вывод с компартментальной эпидемиологической моделью SIR, описывает изменение параметра $\lambda$ во времени, позволяет определять потенциальные контрольные точки, в которых изменяется этот параметр, и делать прогнозы на перспективу.
Следующий раздел содержит некоторые базовые понятия байесовской статистики и краткий обзор методов приближённого байесовского вывода, поэтому его, в принципе, можно пропустить, чтобы перейти к детальному описанию модели.
Байесовский вывод
Задача байесовского вывода — получение апостериорного распределения $p(\boldsymbol{\theta} \vert \mathbf{x})$. Аналитик наблюдает некоторые данные $\mathbf{x} = (x_1, \dots, x_n)$ (реализацию $n$-мерного случайного вектора $\mathbf{X} = (X_1, \dots, X_n)$, где $X_i$ — случайные величины) и хочет что-то узнать о ненаблюдаемых (латентных) параметрах модели $\boldsymbol{\theta} = (\theta_1, \dots, \theta_d) \in \Omega$, моделируемых $d$-мерным вектором случайных величин $\boldsymbol{\Theta} = (\Theta_1, \dots, \Theta_d)$. При этом у него имеются некие соображения на счет того, какими они могут быть $p(\boldsymbol{\theta})$. Кроме того, он может судить о том, как хорошо наблюдаемые данные $\mathbf{x}$ описываются моделью с параметрами $\boldsymbol{\theta}$. Выражается это через правдоподобие $p(\mathbf{x} \vert \boldsymbol{\theta})$ — вероятность наблюдать данные при заданных параметрах. В соответствии с теоремой Байеса апостериорное распределение вычисляется как:
Здесь $p(\mathbf{x} \vert \boldsymbol{\theta})$ — правдоподобие (likelihood) — оценка адекватности предполагаемого значения $\boldsymbol{\theta}$, выражаемая в вероятности наблюдать данные $\mathbf{x}$ при условии выбранной гипотезы для $\boldsymbol{\theta}$. Если компоненты случайного вектора $\mathbf{X}$ независимы и имеют одинаковое распределение (i.i.d.), то правдоподобие для его реализации $\mathbf{x}$ вычисляется как произведение соответствующих правдоподобий для всех $x_i$:
$p(\boldsymbol{\theta})$ — априорное распределение (prior), или то, что известно о параметрах $\boldsymbol{\theta}$ до получения данных. Оно может быть как неинформативным (uninformative prior), если о параметрах мало что известно, и мы не хотим, чтобы наши предположения сильно влияли на результат байесовского вывода, так и информативным (informative prior), если о возможных значениях параметров известно достаточно много (например, пределы принимаемых значений) и нужно, чтобы это было учтено при выводе апостериорного распределения. $p(\boldsymbol{\mathbf{x}})$ — вероятность данных или свидетельство (evidence) того, что эти данные могут быть получены, будет подробно рассмотрено далее. Совместная (joint) плотность распределения данных и параметров модели разбивается на множители $p(\mathbf{x}, \boldsymbol{\theta}) = p(\mathbf{x} \vert \boldsymbol{\theta}) p(\boldsymbol{\theta})$в соответствии с 🔗 цепным правилом/правилом произведения (chain/product rule).
Полный байесовский вывод даже в слегка нетривиальных моделях зачастую затруднён тем обстоятельством, что априорное распределение параметров $p(\boldsymbol{\theta})$ не является сопряжённым семейству функций правдоподобия $p(\mathbf{x} \vert \boldsymbol{\theta})$. Использование сопряжённых семейств распределений существенно упрощает вычисление апостериорных вероятностей в байесовской статистике, так как позволяет заменить вычисление громоздких интегралов в формуле Байеса простыми алгебраическими манипуляциями над параметрами распределений. Громоздким интегралом в формуле Байеса является знаменатель (нормировочная константа) $p(\mathbf{x})$, который в соответствии с правилом суммы (sum rule, law of total probability) вычисляется как:
Т.е. вероятность данных $p(\mathbf{x})$ вычисляется путем интегрирования совместной плотности распределения параметров модели и данных $p(\mathbf{x}, \boldsymbol{\theta})$ по всем возможным значениям параметров $\Omega$ (маргинализация), поэтому $p(\mathbf{x})$ также называют маргинальным (предельным) правдоподобием (marginal likelihood). Но и это ещё не всё. Предельное правдоподобие в байесовской статистике также известно, как априорное прогнозное распределение (prior predictive distribution), поскольку оно определяет наши представления о вероятности данных до того, как будут сделаны какие-либо наблюдения. Это распределение данных, рассчитываемое взвешенным усреднением по всем возможным значениям параметров, веса при этом определяются априорным распределением. Проще говоря, априорное прогнозное распределение представляет собой математическое ожидание правдоподобия $p(\mathbf{x} \vert \boldsymbol{\theta})$, вычисляемое по априорному распределению параметров $p(\boldsymbol{\theta})$ (третья строка в формуле выше).
Подынтегральная функция $p(\mathbf{x}, \boldsymbol{\theta})$ не всегда является интегрируемой в конечном виде. Казалось бы, можно вычислить этот интеграл методом численного интегрирования, но такой способ также быстро становится неосуществимым при увеличении размерности (числа параметров модели). Но, как известно, если интеграл в пространстве высокой размерности невозможно вычислить аналитически, то говорить о его численном вычислении с приемлемой точностью тоже не приходится. Для сопряжённых же семейств распределений этот интеграл можно вычислить аналитически всегда, но встречается такое только в тривиальных моделях. Поэтому в большинстве практических случаев апостериорное распределение известно нам лишь вплоть до некоторой (неизвестной) нормировочной константы:
Для получения приближения на апостериорное распределение $p(\boldsymbol{\theta} \vert \mathbf{x})$ в случаях, когда интеграл в знаменателе теоремы Байеса аналитически невычислим, используется приближённый байесовский вывод.
Помимо вывода параметров модели часто возникает необходимость предсказания новых наблюдений. Т.е. на основе имеющейся реализации $\mathbf{x}$ случайного вектора $\mathbf{X}$ необходимо предсказывать значение $\tilde{x}$ новой случайной величины $\tilde{X}$. Для этого необходимо использовать так называемое апостериорное прогнозное распределение 🧙🏼♂️ (posterior predictive distribution) $p(\tilde{x} \vert \mathbf{x})$, позволяющее определить вероятность нового наблюдения $\tilde{x}$ с учетом уже имеющихся данных $\mathbf{x}$.
Вычисляется это распределение опять же путём интегрирования по всем возможным значениям параметров $\Omega$ совместной плотности вероятности для $\tilde{X}$ и $\boldsymbol{\Theta}$, обусловленной имеющимися наблюдениями $p(\tilde{x}, \boldsymbol{\theta} \vert \mathbf{x})$:
Во второй строчке здесь используется известное нам цепное правило. Равенство в третьей строке справедливо при условии, что новое наблюдение не зависит от предыдущих данных (это значительно упрощает вычисления). Также как и априорное прогнозное распределение, апостериорное прогнозное распределение вычисляется путём взвешенного усреднения правдоподобия по параметрам модели (четвёртая строка). Однако, в отличие от априорного прогнозного распределения, математическое ожидание для $p(\tilde{x} \vert \boldsymbol{\theta})$ теперь является условным (обусловлено наблюдаемыми данными $\mathbf{X}=\mathbf{x}$) и вычисляется по апостериорному распределению параметров $p(\boldsymbol{\theta} \vert \mathbf{x})$.
Апостериорное прогнозное распределение учитывает неопределенность оценок параметров модели $\boldsymbol{\theta}$, которая количественно определяется апостериорным распределением $p(\boldsymbol{\theta} \vert \mathbf{x})$, иначе говоря, представляет собой усреднение множества условных прогнозов по апостериорному распределению параметров.
Очевидно, что интеграл для апостериорного прогнозного распределения $p(\tilde{x} \vert \mathbf{x})$ также в большинстве практических случаев тяжело вычислить аналитически или численно, поскольку в него в явном виде входит апостериорное распределение $p(\boldsymbol{\theta} \vert \mathbf{x})$, трудности в вычислении которого были рассмотрены нами ранее, и интегрирование также осуществляется в пространстве высокой размерности. Здесь впору вспомнить про приближённый байесовский вывод.
Как известно, для приближённого байесовского вывода есть две основных группы методов:
- методы вариационного байесовского вывода (Variational Inference, VI);
- методы Монте-Карло по схеме Марковских цепей (Markov Chain Monte Carlo, MCMC).
Если коротко, то вариационный байесовский вывод — это попытка аппроксимировать апостериорное распределение более простым, которое можно в явном виде посчитать, минимизируя некоторую метрику (дивергенцию Кульбака-Лейблера). В результате задача байесовского вывода (интегрирования в многомерном пространстве) сводится к задаче стохастической оптимизации.
MCMC-семплинг в явном виде доступ к апостериорному распределению не даёт, но даёт возможность генерации репрезентативной выборки из этого распределения, по которой затем можно получать несмещённые оценки любой статистики (в частности вычислять матожидания). Вариационный вывод таких гарантий не даёт, но зато он хорошо масштабируется на большие данные (MCMC-семплинг гораздо более сложен в вычислительном плане).
Эпидемиологических данных достаточно мало, количество новых заболевших — это всего лишь одна цифра в день, поэтому MCMC-семплинг должен отработать за приемлемое время. Выбор очевиден. Для наглядного экспресс ознакомления с основными принципами MCMC-методов можно почитать эту статью, читается относительно быстро, формул там нет.
Методы приближённого байесовского вывода имеют множество реализаций в различных фреймворках вероятностного программирования: PyMC3, TensorFlow Probability, Pyro, Stan, Edward и др. PyMC3 — самый популярный выбор, несмотря на то, что его основной бэкенд Theano уже мёртв 💀, но PyMC4 с TensorFlow Probability в качестве бэкенда уже на подходе. PyMC3 имеет подробную документацию и давнюю историю. Реализация MCMC-метода из PyMC3, точнее его усовершенствованного аналога NUTS 🥜 (No-U-Turn Sampling), в частности использовалась в рассмотриваемой нами немецкой статье. Неплохой обзор этого и других фреймворков вероятностного программирования можно посмотреть тут.
SIR 2.0. Продолжение
Вновь вернёмся к немецкой статье. Т.к. набор эпидемиологических данных — количество новых заболевших в день — является дискретным ($\Delta t=1$ день), то рассмотренная выше система ДУ SIR может быть переписана в виде разностных уравнений ($dI/dt \approx \Delta I / \Delta t$):
Здесь $I_{t}$ и $R_{t}$ — текущее количество болеющих и переболевших соответственно по состоянию на день $t$, $I_{t}^{new}$ и $R_{t}^{new}$ — количество новых заболевших и переболевших соответственно в день $t$.
Количество новых заболевших, которые попадают в официальную статистику в день $t$ определяется в этой модели как $I_{t-D}^{new}=c_t$, где $D$ — задержка (delay) между фактическим инфицированием индивида и его попаданием в официальную статистику заболевших. Параметр $D$ имеет три основных составляющих:
- биологический инкубационный период для COVID-19 с оцениваемым медианным значением порядка пяти дней, по прошествии которого начинают проявляться симптомы заболевания;
- время, в течение которого заболевший терпит симптомы 🤒, прежде чем сделать тест (от одного до трёх дней);
- время, через которое результат проведённого теста становится известен (от одного до четырёх дней), после чего заболевший попадает в официальную статистику.
Не стоит удивляться такой значительной последней составляющей, ведь основным методом диагностики является полимеразная цепная реакция (ПЦР 🧬). Даже после получения положительного результата экспресс-теста, как правило, проводится ПЦР, диагноз уточняется в референс-центре. Сам ПЦР-тест длится около пяти часов, плюс время транспортировки образцов в лабораторию, к тому же не следует забывать про её загруженность.
Как уже говорилось, получение байесовских оценок (распределений) для основных параметров эпидемиологической модели, вектора случайных величин $\boldsymbol{\Theta} = (\lambda_1, \dots, \lambda_k,$ $t_1, \dots, t_k,$ $\Delta t_1, \dots, \Delta t_k,$ $\mu, D, \sigma,I_0)$, осуществляется в рассматриваемой модели с помощью приближённого байесовского вывода (метод MCMC). Модель предполагает возможность изменения эффективной частоты контактов между индивидами в окрестностях некоторых точек $t_i$, $i=1,\dots,k$. При этом предполагается линейное изменение параметра от $\lambda_{i-1}$ до $\lambda_0$ в течение $\Delta t_i$ дней. Важным отличием в текущей версии модели от той, что была использована в статье, является то, что теперь точка $t_i$ должна соответствовать середине этого линейного перехода, в то время как в статье она соответствовала началу перехода. Здесь $\lambda_i$ — эффективная частота контактов между индивидами, достигаемая после окончания мероприятия ко времени $t_i + \Delta t_i/2$. Состав случайного вектора $\boldsymbol{\Theta}$ в нашем случае также немного отличается от представленного в статье (иключены параметры $f_{\omega}$ и $\Phi_{\omega}$), поскольку мы не будем использовать модуляцию количества новых новых случаев заболевания модулем синусоиды, позже увидим почему.
На каждом шаге MCMC в модели предлагается новая реализация параметров $\boldsymbol{\theta}$, на основе которой генерируется временной ряд (детерминированный), описывающий вектор количества новых случаев заражений $\tilde{\mathbf{c}}(\boldsymbol{\theta}) = \left\{ \tilde{c_t}(\boldsymbol{\theta}) \right\}$ той же длины, что и наблюдаемые на текущий момент данные $\mathbf{c} = \left\{ c_t \right\}$ (такие обозначения используются для сохранения совместимости со статьёй 🔨). Это так называемый предиктивный вывод (predictive inference), при котором используется семплирование из рассмотренного нами ранее апостериорного прогнозного распределения $p(\tilde{\mathbf{c}} \vert \mathbf{c})$. Затем полученная реализация $\boldsymbol{\theta}$ либо добавляется в выборку для $\boldsymbol{\Theta}$, либо отклоняется. Это продолжается до тех пор, пока полученная выборка не будет хорошо описывать апостериорное распределение:
Здесь, в полном соответствии с предыдущим разделом, $p(\boldsymbol{\theta} \vert \mathbf{c})$ — апостериорное распределение, $p(\mathbf{c} \vert \boldsymbol{\theta})$ — правдоподобие, $p(\boldsymbol{\theta})$ — априорное распределение.
Правдоподобие $p(\mathbf{c} \vert \boldsymbol{\theta})$ в модели представляет собой произведение правдоподобий для всех $c_t$ (вспоминаем про i.i.d.), каждое из которых имеет вид:
Это распределение Стьюдента (t-распределение). У него довольно интересная история, тесно связанная с пивоварней 🍺 Гиннесс в Дублине (Википедия знает всё). График плотности t-распределения на первый взгляд похож на плотность нормального распределения, он также является симметричным и имеет вид колокола, но хвосты у него более «тяжёлые», т.е. реализациям случайной величины, имеющей распределение Стьюдента, более свойственно сильно отличаться от математического ожидания (количество $c_t$ новых заболевших в день $t$ подходит под это описание).
Для прогнозирования количества новых заболевших на следующий за последним днём в наборе данных день (и на другие дни после него), необходимо взять все полученные выборки, характеризующие апостериорное распределение $p(\boldsymbol{\theta} \vert \mathbf{c})$, и продолжить дальнейшее интегрирование системы ДУ SIR во времени. В результате получаем ансамбль прогнозов для количества новых заболевших на каждый последующий день, или апостериорное прогнозное распределение — усреднение условных прогнозов по апостериорному распределению параметров модели. При этом объединяются два источника неопределённости: неопределённость параметров $\boldsymbol{\Theta}$ в том виде, в котором она отражается апостериорным распределением, и неопределённость выборки $\mathbf{c}$, заключённая в функции правдоподобия.
Контрольные точки и априорные распределения
Контрольные точки $t_i$ на начальном этапе развития эпидемии, в которых подразумевается изменение эффективной частоты контактов между индивидами $\lambda$, вводятся в модель, исходя из априорной информации о проводимых ограничительных мероприятиях в той или иной стране/городе. Модель может уточнять положение этих точек (по сути обнаруживать их), если указываются широкие временные пределы, в которых они потенциально могут находиться, и адекватные пределы для возможных значений $\lambda_i$.
В немецкой статье обнаруженные моделью контрольные точки практически полностью совпали с мероприятиями проводимыми правительством Германии. Так, в начале марта были отменены крупные публичные мероприятия (матчи Бундеслиги⚽️ проводились уже без зрителей), с 16 марта закрыты детские сады, школы, вузы, с 23 марта — большинство магазинов, бары, клубы, театры, концертные залы, музеи, бассейны и фитнес-центры, рестораны и кафе, отели, парикмахерские, салоны красоты и др. Гражданам разрешается свободно выходить на улицу для проезда на работу, в продуктовый магазин, для индивидуальных занятий спортом и прогулок (привет Москве 🚷). Общественные места разрешается посещать только по одному или парой (Kontaktsperre), либо в сопровождении проживающих вместе родственников. За соблюдением данных мер наблюдает полиция, в некоторых федеральных землях, например, в Берлине, нарушителям грозят большие штрафы. В результате количество новых регистрируемых случаев заболевания начало устойчивое снижение уже через две недели. У нас, к сожалению, тотальный режим самоизоляции, введённый 30 марта, таким эффективным не оказался…
Посмотрим как с 10 марта по 26 мая выглядела динамика выявления заболевших в Германии 🇩🇪, в России 🇷🇺 и в Москве:
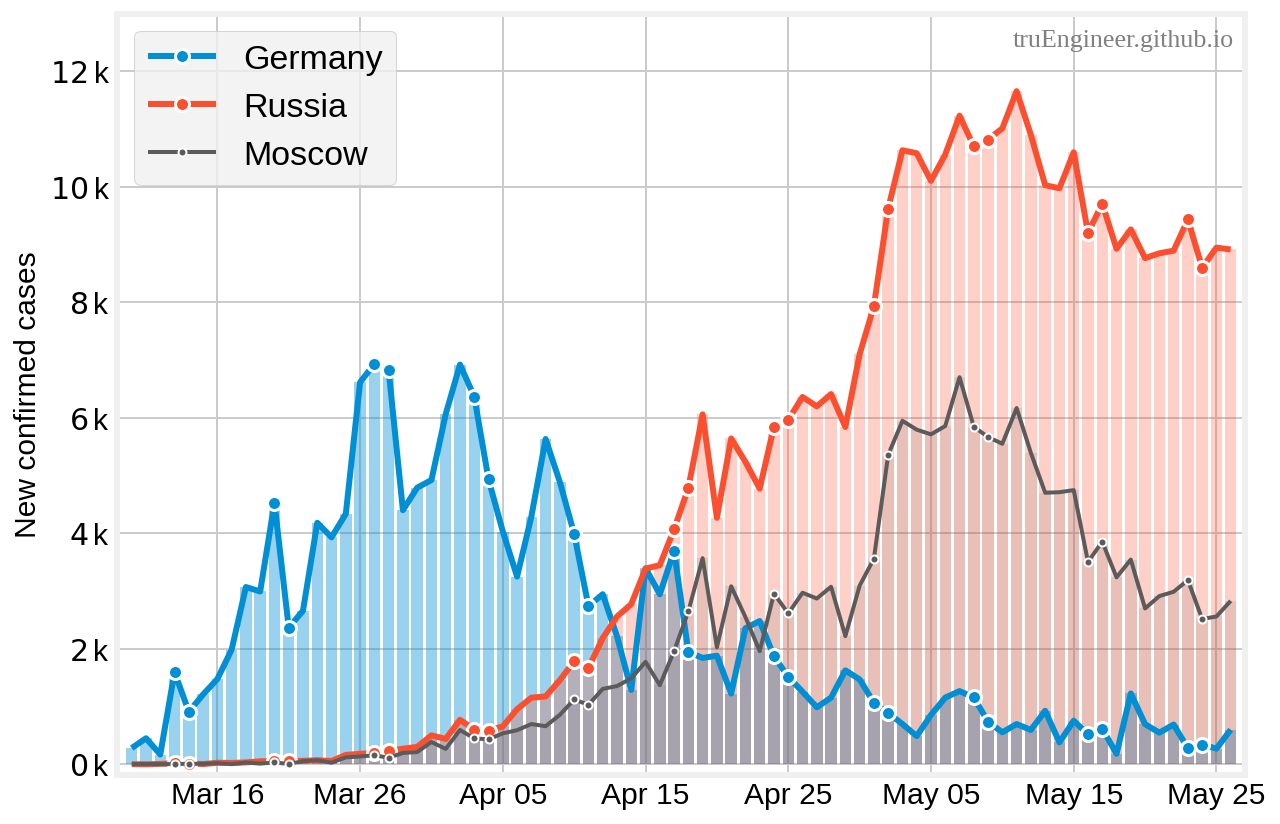
Первое, что бросается в глаза — графики для России и Москвы сильно коррелированы (коэффициент корреляции +0.96). Как-никак, в Москве проживают более 12 миллионов человек и развёрнуто массовое тестирование. Поэтому и количество выявленных случаев COVID-19 значительно превышает таковое в любом другом субъекте РФ.
Что ещё можно сказать по этим графикам? Выходные дни помечены на них круглыми маркер-точками. В Германии, по всей видимости, даже во время эпидемии не забывают о том, что сотрудники тестовых лабораторий должны отдыхать, поэтому количество проводимых тестов в выходные дни обычно меньше, чем в будни. Это отражается на статистике ежедневно выявляемых случаев заболевания, где можно наблюдать локальные минимумы по выходным и максимумы ближе ко вторнику. Именно поэтому в немецкой модели используется ещё пара параметров ($f_{\omega}$, $\Phi_{\omega}$) и соответствующие им априорные распределения для модуляции количества новых регистрируемых случаев модулем синусоиды с периодом около семи дней. В нашем случае такой тенденции не наблюдается (лаборатории работают более хаотично), поэтому эти параметры и были исключены из модели. Может быть такие всплески в статистике, наблюдаемые не только в Германии, но и в других странах (Италия 🇮🇹, США 🇺🇸) — это некий косвенный показатель качества организации тестирования, но об этом пусть судят компетентые люди.
Далее мы будем осуществлять моделирование для Москвы (размер популяции $N$ равен 12 миллионам человек) и использовать данные по количеству ежедневно регистрируемых случаев заболевания за 2 месяца развития эпидемии, с 16 марта по 16 мая (последний день в наборе данных на момент начала нашего моделирования). Также осуществим прогноз на 10 дней, с 17 мая по 26 мая включительно, чтобы потом сравнить с реальными данными. Собственно поэтому 27 мая и пишется 📝 этот пост.
Перейдём теперь непосредственно к заданию априорных распределений для параметров нашей модели. Зададим информативные, но при этом относительно широкие априорные распределения, чтобы была возможность поточнее определить контрольные точки, в которых меняется эффективная частота контактов. Таким образом, априорные распределения должны ограничивать значения, которые могут принимать параметры модели, но вместе с тем должны быть достаточно широкими, чтобы учитывать возможные изменения параметров в широких пределах, как в плюс, так и в минус.
Перед заданием априорных распределений для контрольных точек $t_i$ необходимо определить временные границы, в которых менялась эффективная частота контактов $\lambda$ (темпы заражения). Для этого нужно почитать новости…
Официально Москва начинает борьбу с распространением заболевания ещё 10 марта, когда вводится запрет на массовые мероприятия. Но в целом индекс самоизоляции в течение этой недели не отличался от среднего уровня беззаботного февраля (в среднем 0.3 по будням в Москве). Народ продолжал жить и работать, как обычно 🚇.
Вечером 16 марта на сайте мэра Москвы было объявлено о запрете с 17 марта любых мероприятий с числом участников более 50 человек единовременно, переводе школ на режим свободного посещения и их закрытии к 21 марта. На этой же неделе 18 марта в России вступили в силу ограничения на въезд в страну иностранных граждан и лиц без гражданства. Российская Премьер-Лига 🐻 приостановила матчи, за ней потянулись другие спортивные лиги. Индекс самоизоляции в Москве по будням стал в два раза выше обычного (народу на улицах впервые немного поубавилось).
С 26 марта в Москве предписано соблюдать самоизоляцию гражданам от 65 лет и старше. Также указом мэра с 28 марта по 5 апреля было предписано прекратить работу ресторанов, кафе, баров, столовых и других предприятий общественного питания, розничной торговли, 55 парков, и предприятий сферы услуг. С 30 марта домашний режим самоизоляции был введён для всех жителей Москвы — независимо от возраста. Основаниями для выхода на улицу являются: необходимость присутствия на рабочем месте, покупки в ближайшем работающем магазине или аптеке, выгул домашних животных на расстоянии не более 100 метров от места проживания, вынос мусора, обращение за экстренной медицинской помощью или прямая угроза жизни и здоровью. В этот же день Россия полностью закрывает свои границы 🛂. Индекс самоизоляции в Москве впервые достигает значения больше трёх в будние дни, автомобилисты радуются.
10 апреля в блоге мэра уже сообщалось о том, что около 75% жителей города теперь лишены возможности свободно передвигаться по Москве. В частности закрытие учебных заведений привело к ограничению передвижения двух миллионов человек, а самоизоляция пожилых и хронически больных москвичей добавила к этому числу ещё два миллиона. Также сообщалось, что со следующей недели, то есть с 13 апреля, в Москве поэтапно начнут вводить пропускной режим, и что с 13 по 19 апреля в городе временно останавливается работа практически всех предприятий и организаций. Пропускной режим начал работать 15 апреля, дав образоваться очередям в метро, а с 22 апреля проезд в общественном транспорте города стал возможен только при наличии цифрового пропуска с привязанной к нему транспортной или социальной картой, проверка пропусков была переведена в автоматический режим. Вот и все основные новости марта/апреля по противоковидным мероприятиям в Москве, их мы и будем использовать при задании априорных распределений для контрольных точек.
В немецкой статье подразумевается, что каждое вмешательство правительства как минимум на 50% уменьшает эффективную частоту контактов. Мы будем считать примерно также. Для моделирования большинства параметров будем использовать логнормальное распределение, стандартная практика для обеспечения вычислительной устойчивости вероятностных моделей. Медианное значение для начального значения эффективной частоты контактов $\lambda_0$ возьмём равным 0.4 (как и в немецкой статье). Это достаточно много, чтобы в относительно короткие сроки была инфицирована бОльшая часть популяции. Априорное распределение для случайной величины $\lambda_0$ оставим достаточно широким, СКО для распределения $\log{\lambda_0}$ (нормального распределения) также зададим 0.5, чтобы модель могла уточнить значение $\lambda_0$ в широких пределах.
Априорные распределения для остальных лямбд оставим такими же широкими (СКО для их логарифмов 0.5). Медианное значение для $\lambda_1$ возъмём равным 0.2 (интенсивность новых заражений уменьшается в два раза по сравнению с начальной), а для $\lambda_2$ уменьшим медиану ещё в два раза до 0.1 (началась самоизоляция).
Значение медианы для $\lambda_2$ меньше, чем медиана для интенсивности выбывания $\mu=0.125$ (этот параметр уже оценён во множестве статей и сильно поменяться не должен), т.е. мы подразумеваем, что в целом распространение болезни в окрестностях точки $t_2$ замедляется настолько, что в скором времени должно привести к уменьшению роста числа новых заболевших, т.е. противоковидные мероприятия эффективны.
Как-никак, в окрестностях точек $t_1$, $t_2$ проводились основные ограничительные мероприятия ⛔️. $t_1$ — середина участка с 16 по 21 марта, закрытие школ и других учреждений, $t_2$ — середина участка с 26 марта по 30 марта, от начала самоизоляции для пенсионеров до начала самоизоляции для всех. Точку $t_3$ вводим, исходя из того, что с 13 по 24 апреля в Москве закрывалось большинство организаций/предприятий и с переменным успехом внедрялся пропускной режим, также задаем для неё самое большое СКО, равное трём. Значение медианы для $\lambda_3$ также берём равным 0.1, подразумевая, что хуже от этих мероприятий не стало, и тенденция на снижение темпов заражения сохраняется. Наш сценарий в целом, как и у немцев, оптимистичный.
Медианные значения для длительностей интервалов перехода $\Delta t_i$ положим равными около четырёх дней, чтобы сглаживать возможные выбросы в окрестностях контрольных точек, и примерно соотвествовать длительностям введения ограничительных мер по крайней мере для $t_1$ и $t_2$, положение которых из новостей мы знаем достаточно точно (СКО для обоих распределений берутся равными единице).
Медианное значение для задержки $D$ выберем около 10 дней, СКО для $\log{D}$ возьмём равным 0.2 (стандартные значения, которые берутся во втором репозитории для моделирования эпидемии в федеральных землях Германии). Таким образом, первый перцентиль логнормального распределения для $D$ составляет около шести дней, 99-перцентиль — около 16. Вполне допустимый разброс возможных значений. Напомним, что медианная оценка длительности инкубационного периода для COVID-19 — это что-то около пяти дней, поэтому попасть в официальную статистику заболевших через шесть дней — просто идеальный вариант, рассчитывать на который стоит, если вы каждый день делаете тест 💸.
Для $I_0$ (начального числа заболевших) и $\sigma$ (параметра масштаба для правдоподобия Стьюдента) выберем значения коэффициентов масштаба соответствующих усечённых распределений Коши 100 и 10 соответственно (неинформативные априорные распределения). Начальное количество инфицированных вряд ли превышает 100 человек, а $\sigma$ в целом допускает возможность десятикратного превышения числа заболевших.
Таким образом, априорные распределения для параметров нашей модели выглядят следующим образом:
Здесь $X \sim \mathit{N}(\mu_X,\sigma_X)$ — нормальное распределение случайной величины $X$ с матожиданием $\mu_X$ и СКО $\sigma_X$, $X \sim \mathit{LogN}(\mu_X,\sigma_X)$ — логнормальное распределение с параметрами $\mu_X$ и $\sigma_X$, $X \sim \mathit{HalfC}(\beta_X)$ — усечённое распределение Коши, определенное на положительной полуоси и характеризуемое коэффициентом масштаба $\beta_X$. Формулы соответствующих плотностей вероятностей можно уточнить в разделе документации библиотеки PyMC, посвящённом распределениям непрерывных случайных величин.
Семплирование и прогнозы
Параметры априорных распределений подбирались ещё и с тем учётом, чтобы в используемых нами четырёх chains=4 семплирующих цепочках (в конфигурации tune=1500 отсчётов на «прогрев» цепи, burn-in phase 🔥, sample=1500 отсчётов после выхода цепи на стабильный режим работы, sampling phase) не возникало расхождений, и PyMC не сыпал предупреждениями о неэффективности выборок после их диагностики. По 1500 элементов в каждой цепочке предназначено для автоматической точной настройки алгоритма NUTS. Эта часть выборки затем отбрасывается по умолчанию. Этап точной настройки помогает NUTS формировать надёжную выборку из апостериорного распределения. Далее в каждой цепочке генерируется ещё по 1500 элементов, уже попадающих в итоговую выборку. Таким образом, всего для каждого параметра генерируется итоговая выборка из 6000 элементов. Первичная инициализация марковских цепей ⛓ осуществляется с помощью одного из алгоритмов вариационного вывода (automatic differentiation variational inference, ADVI), апостериорное распределение аппроксимируется нормальными распределениями параметров, при этом возможные корреляции между параметрами игнорируются. Из этой смеси нормальных распределений затем семплируются четыре стартовые точки для марковских цепей.
Запускаем семплирование… Диагностику выборок для интересующих нас параметров в PyMC, после завершения семплирования, можно осуществлять визуально (traceplot), построив графики истории марковских цепей. Анализируя их, можно понять, насколько хорошо отработал алгоритм семплинга и требует ли он дополнительной настройки. Визуальными критериями качества являются:
- стационарность, т.е. элементы выборок должны образовывать шум около какого-то значения;
- выборки не должны иметь сильно выраженной автокорреляции;
- история цепи не может состоять из одной и той же повторяющейся точки (быть практически постоянной).
Внизу слева изображены графики ядерной оценки плотности апостериорных распределений (напомним, что мы задавали логнормальное априорное распределение для $\mu$, и нормальные априорные распределения для логарифмов $\lambda_i$), по сути это сглаженные версии гистограмм оцениваемых моделью параметров. Справа приведены непосредственно значения элементов выборки (история марковских цепей) на каждом шаге процесса семплирования (1500 семплов на каждую из четырёх цепей, т.е. 6000 семплов для каждого параметра):
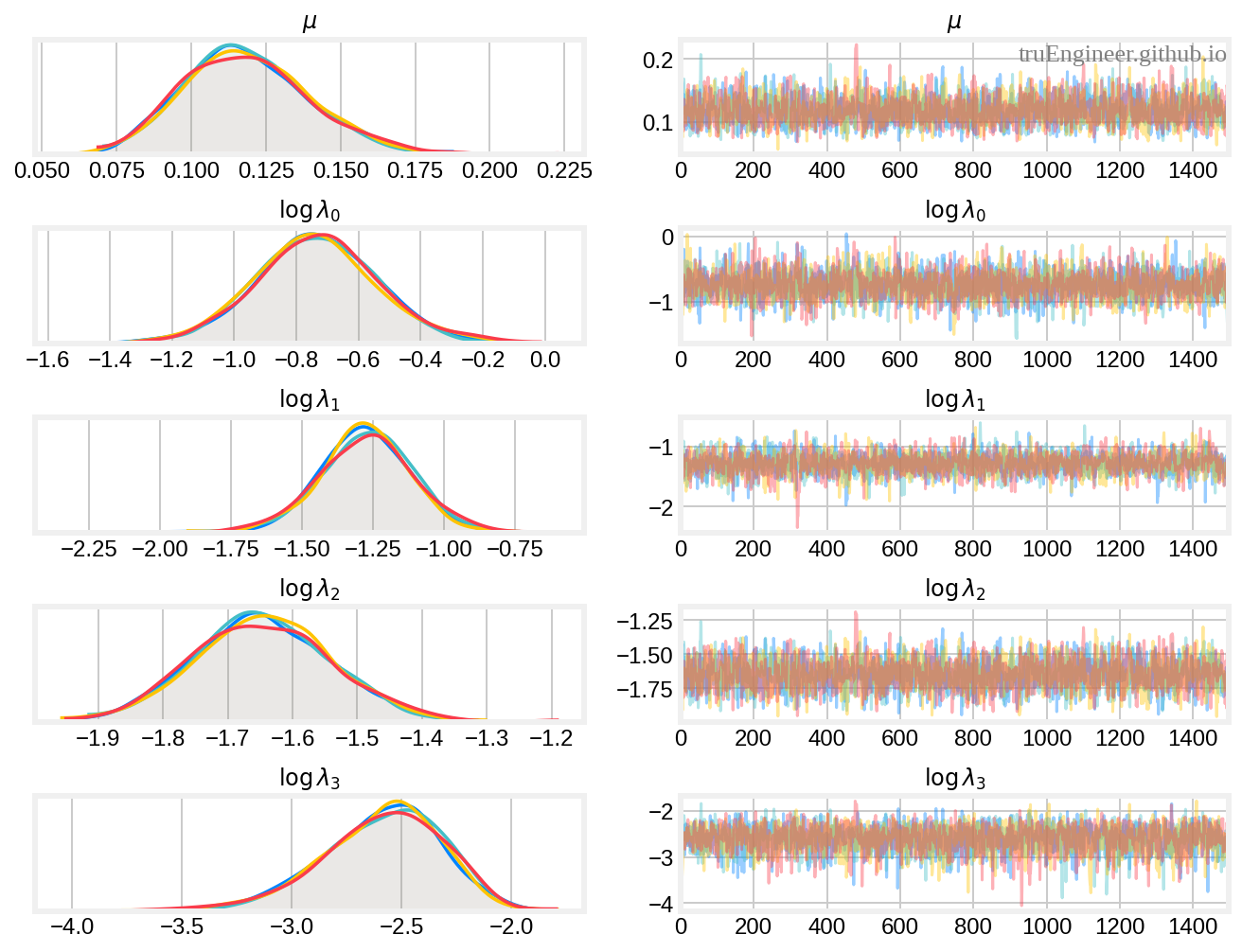
Всё выглядит вполне неплохо.
Помимо визуальной диагностики, автоматически рассчитывается много диагностических статистик, одной из которых является $\hat R$ (r-hat) статистика — результат сравнения дисперсий внутри цепей с дисперсиями между цепями. Для всех параметров, оцениваемых моделью, она составила величину 1.0, что говорит о сходимости (convergence) алгоритма семплирования (получена хорошая выборка из апостериорного распределения).
Для удобства диагностики модели и оценки адекватности выбора априорных распределений построим гистограммы для основных параметров, оцениваемых моделью. Для всех случайных величин с логнормальным распределением (кроме $\mu$) будем расcчитывать гистограммы для их логарифмов, т.е для нормальных распределений:
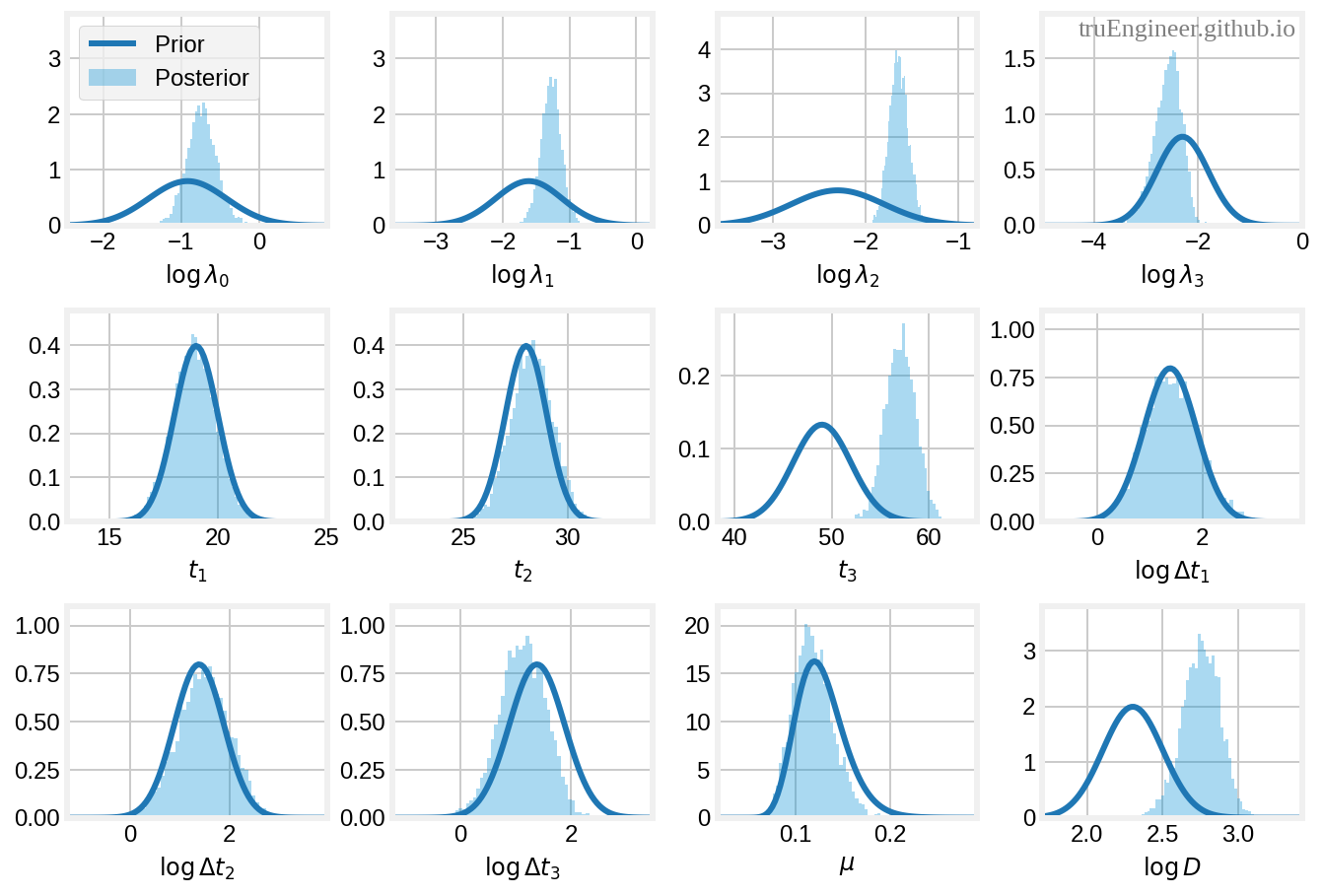
Как видим, в то время как мы ввели довольно широкие априорные распределения для эффективных частот контактов $\lambda_i$ (и, соответственно, для их логарифмов), мы получили сравнительно узкие апостериорные распределения для логарифмов каждой из них. Широкие априорные распределения сделали своё дело. Апостериорные распределения для первых двух контрольных точек ($t_1$ и $t_2$) легли в соответствующие априорные распределения (новости не врут). Мода апостериорного распределения для третьей контрольной точки $t_3$, с самым широким априорным распределением, расположена в районе 99-перцентиля априорного распределения для $t_3$ (эту точку наша модель, по сути обнаружила). Распределение для интенсивности выбывания $\mu$ соответствует априорному, т.е. соответствует имеющимся оценкам $\mu$ для COVID-19. Медианные значения и байесовские доверительные интервалы (credible intrvals, CI) для всех параметров, оцениваемых моделью (в особенности для времени задержки $D$), будут рассмотрены нами далее.
Взглянем, наконец, на основные результаты работы модели. Аппроксимация имеющихся данных с доверительным интервалом 95% и прогноз 🔮 на 10 дней с доверительными интервалами 75% и 95% выглядят следующим образом:
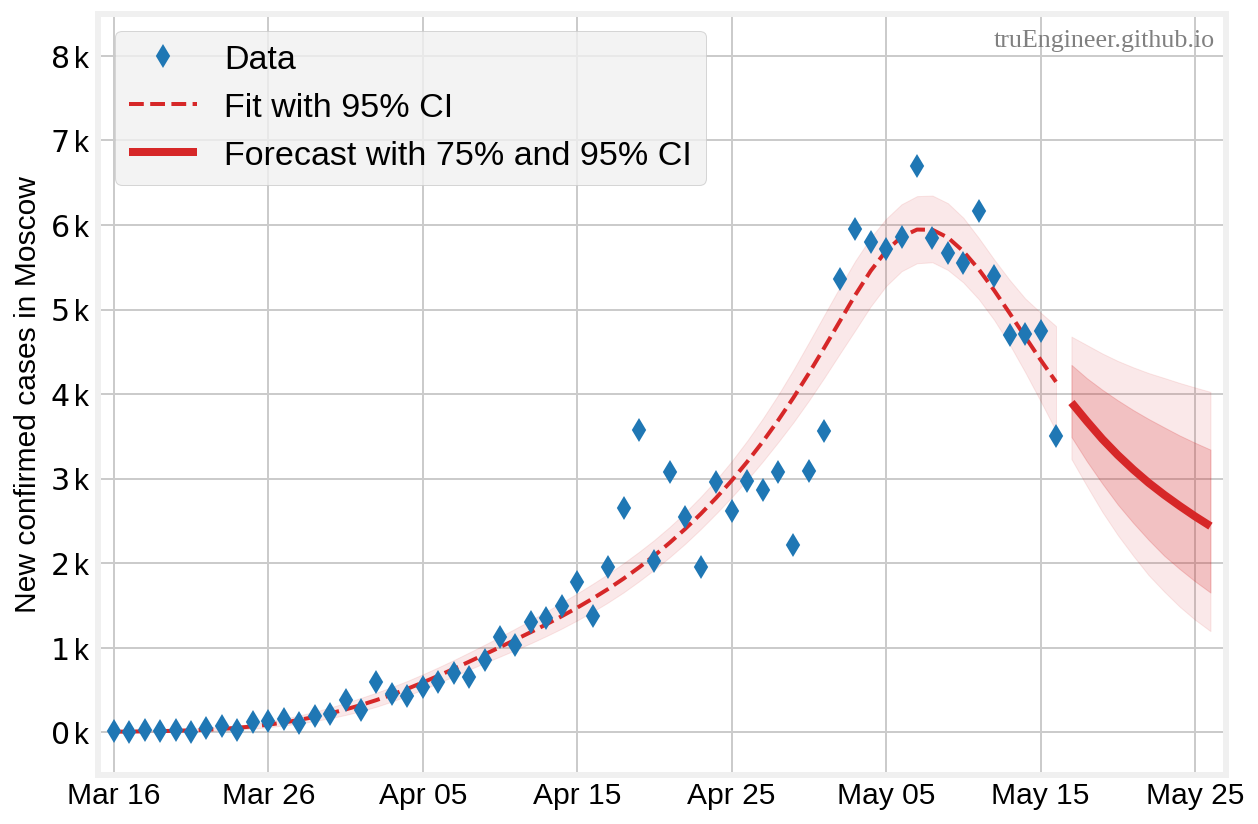
Красная пунктирная линия на графике соответствует медиане (50-му перцентилю) апостериорных прогнозных распределений числа новых регистрируемых случаев заболевания для каждого из дней в наборе данных — аппроксимация данных (fit). Чтобы аппроксимация лучше соответствовала реальным данным можно, конечно, ввести ещё несколько контрольных точек (особенно в районе 15-30 апреля) с относительно малоинформативными априорными распределениями (медианные значения для соответствующих $\lambda_i$ считать равными 0.1), но обучать такую модель будет сложнее, ведь набор данных относительно мал, а качество прогнозов при этом, скорее всего, ухудшится. В целом наша модель сглаживает выбросы и адекватно описывает данные.
Теперь перейдём к оценке непосредственно прогнозных способностей модели. На графике выше сплошной красной линией представлены медианные оценки прогнозируемого числа новых заболевших на 10 дней (с 17 по 26 мая). Эти медианные оценки (forecast), соответствующие им 75% доверительные интервалы (75% CI) апостериорных прогнозных распределений и реальные цифры заболевших в эти дни (real data) представлены в таблице:
| date | forecast | 75% CI | real data | error |
|---|---|---|---|---|
| May 17 | 3903 | [3488, 4366] | 3855 | 48 |
| May 18 | 3678 | [3200, 4217] | 3238 | 440 |
| May 19 | 3470 | [2934, 4088] | 3545 | 75 |
| May 20 | 3280 | [2688, 3964] | 2699 | 581 |
| May 21 | 3103 | [2464, 3854] | 2913 | 190 |
| May 22 | 2941 | [2259, 3750] | 2988 | 47 |
| May 23 | 2796 | [2077, 3654] | 3190 | 394 |
| May 24 | 2659 | [1915, 3557] | 2516 | 143 |
| May 25 | 2537 | [1769, 3472] | 2560 | 23 |
| May 26 | 2420 | [1636, 3388] | 2830 | 410 |
В пятом столбце таблицы — значения абсолютной ошибки (error) между прогнозом и реальными данными (медиана апостериорного распределения минимизирует ожидаемые абсолютные потери). Средняя абсолютная ошибка (mean absolute error, MAE) в прогнозе на 10 дней составила величину 235.1, а все реальные данные попали в 75% доверительный интервал для полученных прогнозов, из чего можно судить, что модель справилась с задачей довольно неплохо 🤖 (плюс ещё, конечно, повезло, что в Москве за эти 10 дней не было выявлено никаких крупных очагов инфекции, и тенденция на снижение заболеваемости продолжилась).
В полном соответсвии с байесовской логикой, чем больше данных и меньше количество дней, на которое делается прогноз, тем меньше доверительный интервал апостериорного прогнозного распределения. На графиках ниже представлены прогнозы, полученные моделью на основе имеющихся по состоянию на 16, 18, 20, 22 и 24 мая данных, на 10, 8, 6, 4 и 2 дня соответсвенно (все прогнозы начинаются от дня, следующего за последним днём в наборе данных, а заканчиваются 26 мая):
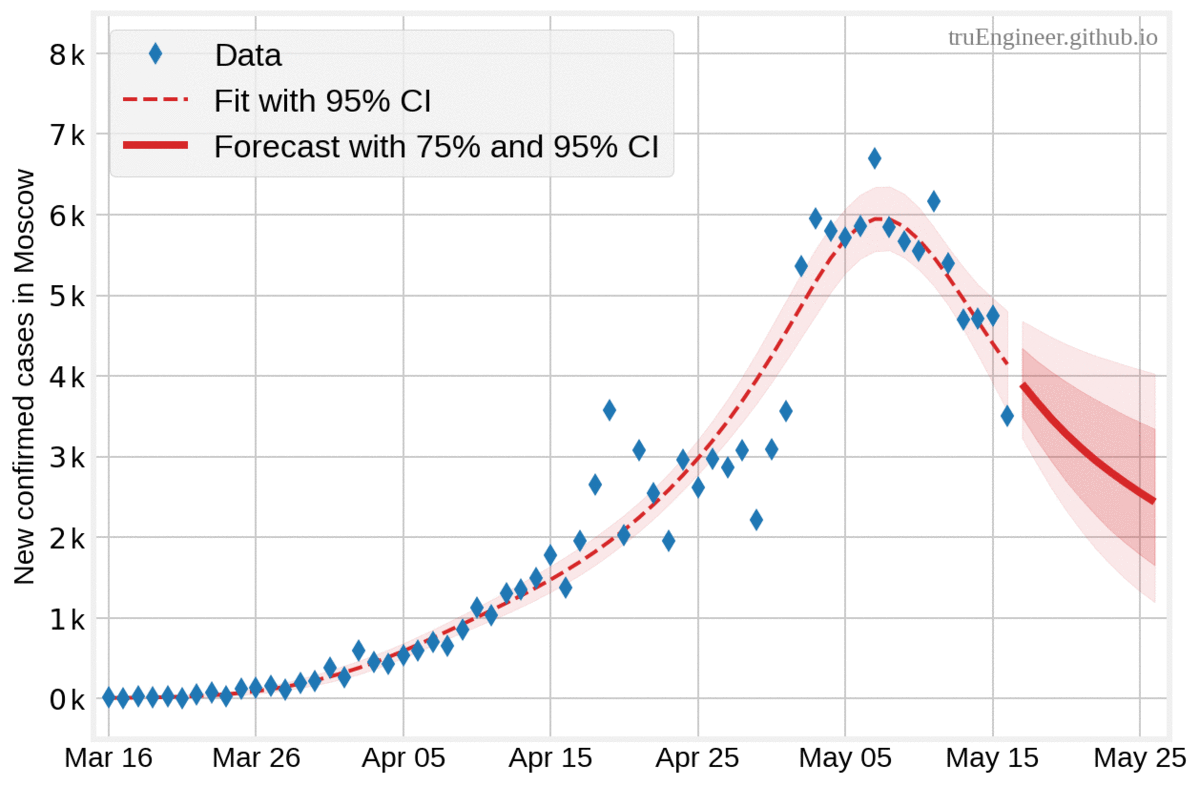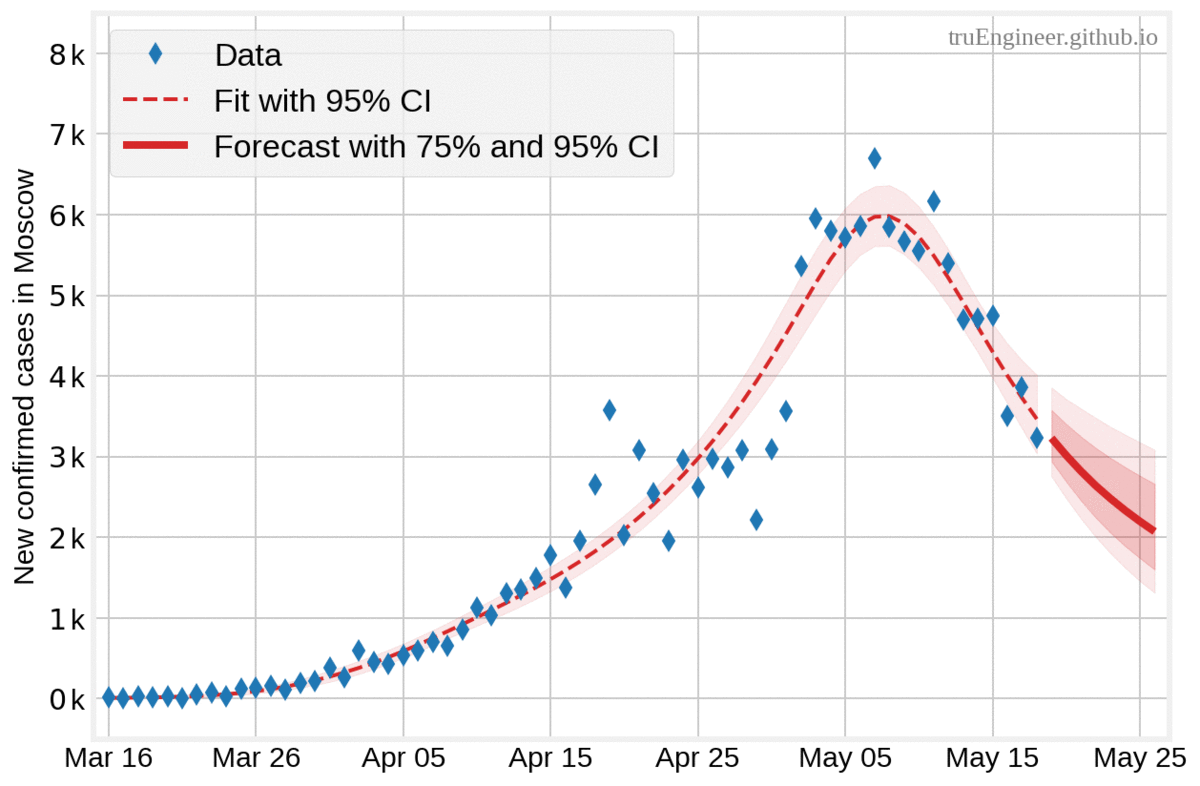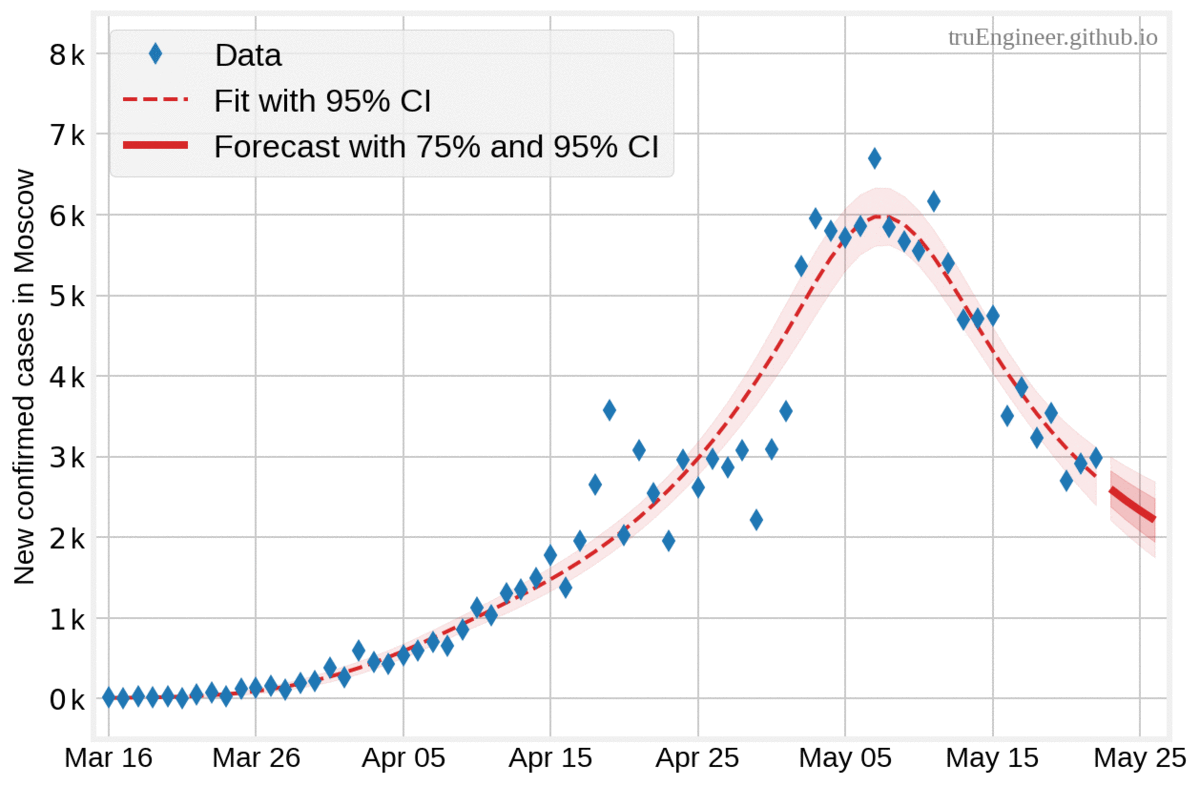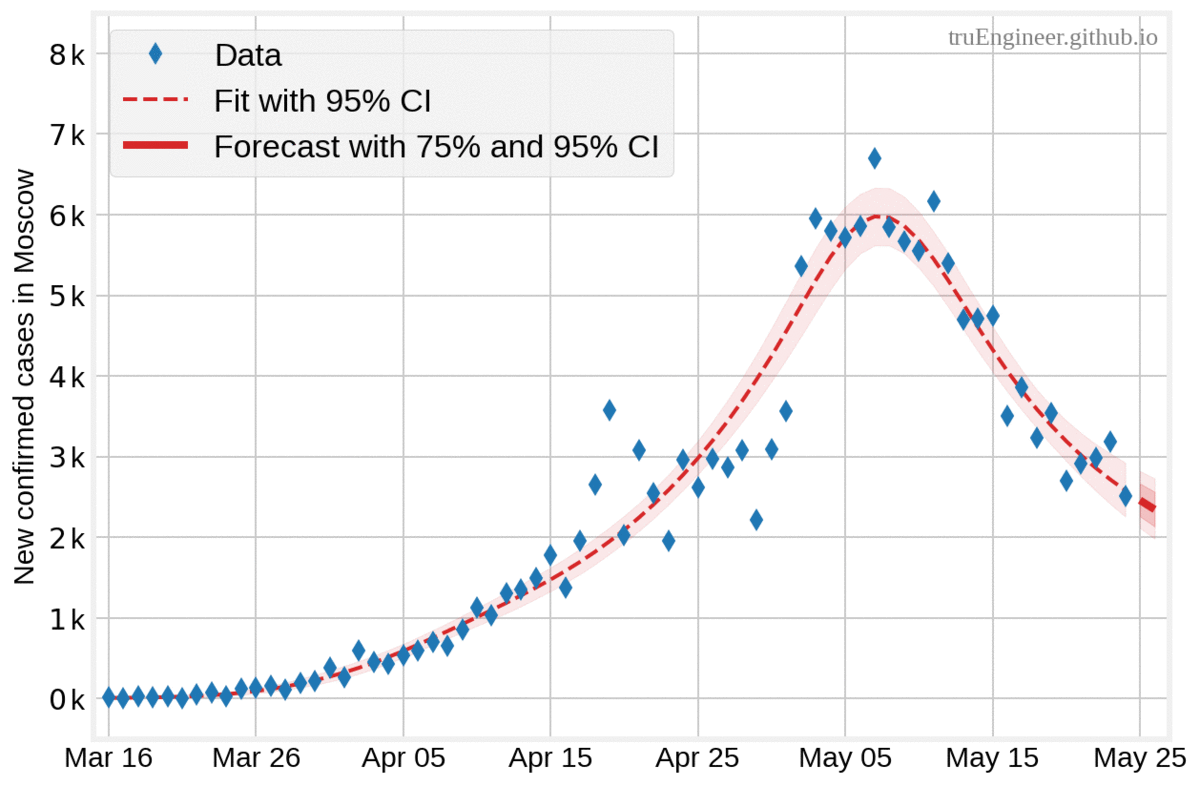
Интерпретация байесовского доверительного интервала весьма интуитивна. Для оцениваемого параметра это числовой интервал, покрывающий значения этого параметра с заданной апостериорной вероятностью. Проще говоря, байесовский 75% доверительный интервал $[100, 500]$ для ненаблюдаемого оцениваемого параметра (случайной величины) означает, что значение оцениваемого параметра с вероятностью 75% попадёт в пределы этого интервала. Люди зачастую неправильно воспринимают частотные (фреквентистские) доверительные интервалы (confidence intervals), как байесовские доверительные интервалы, хотя в первом случае границы интервала являются случайными величинами, а оцениваемый параметр — нет. Фреквентистский 75% доверительный интервал означает, что при большом числе испытаний (случайных экспериментов) с одинаковым правилом построения доверительного интервала (интервалы отличаются друг от друга), 75% таких рассчитанных доверительных интервалов будут содержать истинное значение параметра.
Теперь взглянем на гистограммы апостериорных плотностей вероятностей для основных оцениваемых моделью параметров (соответствующие параметрам медианные оценки, 95% доверительные интервалы и априорные распределения также представлены на графиках):
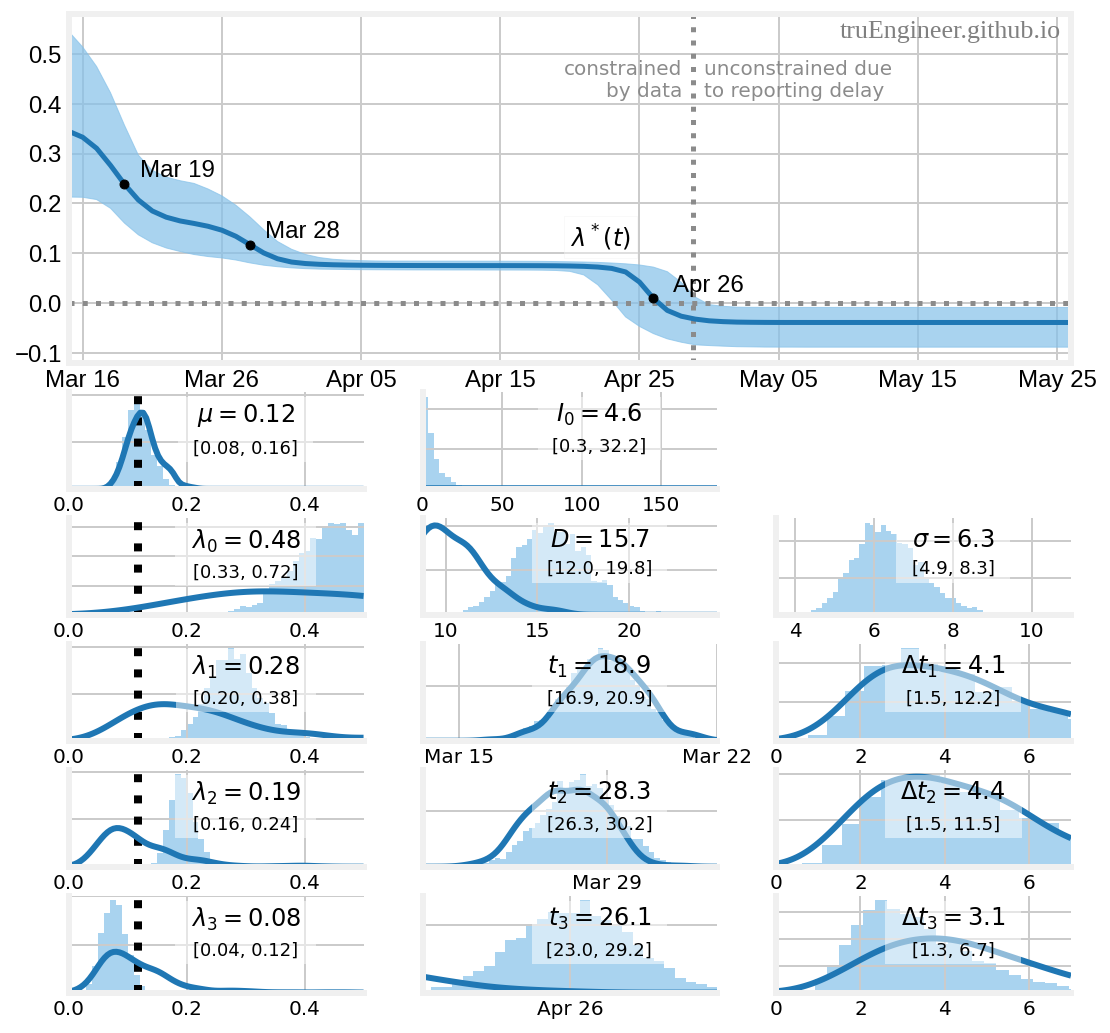
График апостериорного прогнозного распределения для текущего темпа прироста заболевших (effective growth rate, разность между текущим значением эффективной частоты контактов и интенсивностью выбывания) $\lambda^{\ast}(t)=\lambda(t)-\mu$ в верхней части рисунка примерно показывает, как параметр $\lambda^{\ast}$ изменялся с течением времени в рамках рассматриваемой модели. Это три участка линейного изменения, в течение которых $\lambda_{i-1}$ переходит к $\lambda_i$ ($i=1, \dots, 3$), точки $t_i$ — середины этих участков (определены моделью) — отмечены на графике чёрными маркерами. В течение первого такого линейного участка частота контактов изменяется от $\lambda_1 = 0.48$ до $\lambda_1 = 0.28$. Последний день первого участка $t_1 + \Delta t_1/2$ соответствует 21 марта (оценённое медианное значение для $\Delta t_1$ около четырёх дней). К этому дню как раз закрылись все школы. К середине дня 30 марта ($t_2 + \Delta t_2/2 = 30.5$), эффективная частота контактов становится равной $\lambda_2 = 0.19$. Тут уже заработала самоизоляция. Наконец, третий участок, заканчивается, согласно результатам моделирования, где-то в середине дня 27 апреля. Апостериорное распределение для $\lambda_3$ находится левее вертикальной чёрной пунктирной линии, соответствующей медиане апостериорного распределения для интенсивности выбывания $\mu$. Именно эта точка и является переломным моментом, когда эффективная частота контактов $\lambda_3$ становится меньше чем интенсивность выбывания $\mu$.
Нетрудно заметить, что моды апостериорных распределений для $t_3$ (медиана 26 апреля) и $D$ (медиана 15.7 дней) находятся в районе 99-х перцентилей выбранных для них априорных распределений, это в целом приемлемо, но можно попробовать уточнить эти параметры. Учитывая, что оценка параметра $D$ сильно зависит от выбора контрольных точек (в частности от $t_3$, для которой у нас нет такой чёткой временной привязки из новостей, как для $t_1$ и $t_2$), имеет смысл изменить априорное распределение для $t_3$, чтобы уточнить положение этой контрольной точки во времени. Таким образом, оставив априорные распределения для других параметров неизменными, сместим центр поисков к 26-му апреля и зададим СКО априорного нормального распределения для $t_3$ равным двум: $t_3 \sim \mathit{N}\, (26/04/2020, 2)$, после чего вновь запустим семплирование… После завершения расчётов, построим гистограммы для основных параметров модели:
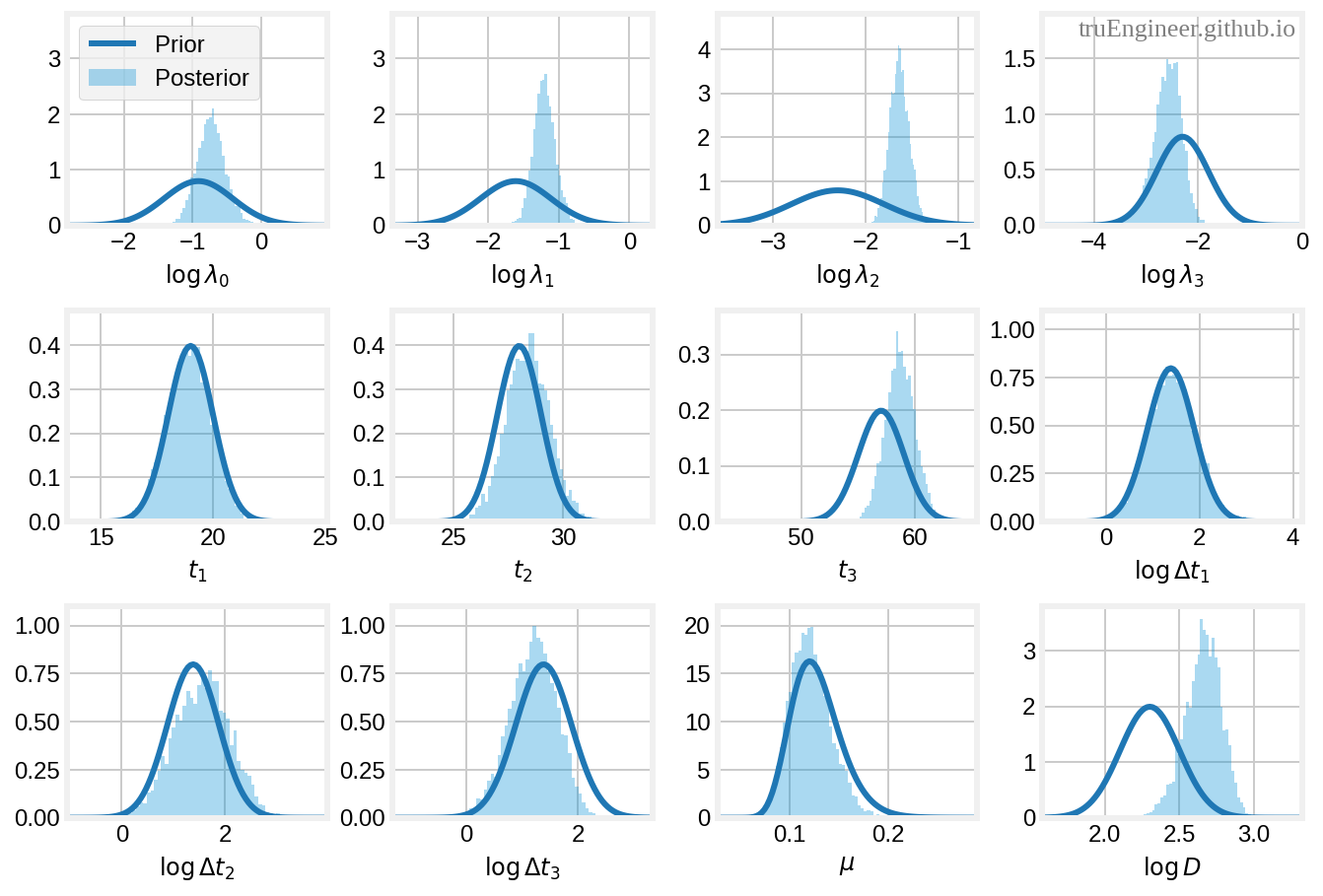
Как видим, мода апостериорного распределения для $t_3$ теперь находится в районе 85-го перцентиля априорного распределения. Оценка для $D$ также немного изменилась. Результаты, полученные новой моделью, представлены ниже на рисунке:
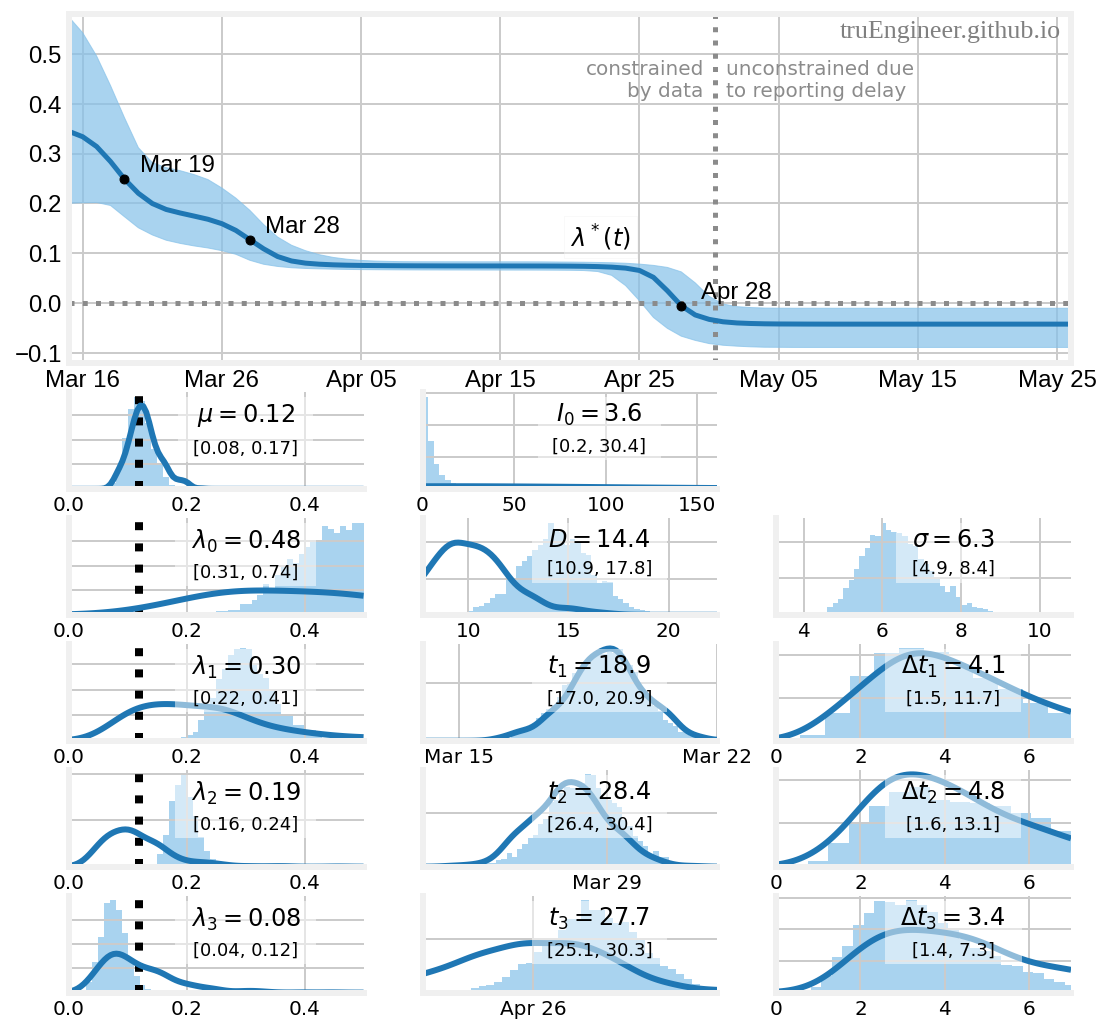
Медианная оценка времени завершения третьего участка изменения эффективной частоты контактов $\lambda$ (или текущего темпа прироста больных $\lambda^{\ast}$) теперь соответствует примерно середине дня 29 апреля ($t_3 + \Delta t_3/2 = 29.4$) Что же произошло к этому дню? Ему много чего предшествовало: и множественные эксперименты мэрии Москвы с пропусками, и очереди в метро, и наращивание скрининговых мощностей, речь о котором пойдет в следующем разделе. В любом случае, после завершения третьего участка 29 апреля, примерно через две недели (медианная оценка $D=14.4$) большинство фактически инфицированных в дни около точки $t_3$ попали в официальную статистику заболевших 🚑, и в районе 12-14 мая начался спад на графике ежедневно регистрируемых случаев заболевания. Вполне правдоподобно.
Рассуждения о тестировании
Почему введённые у нас ограничительные меры не отработали также, как в немецком сценарии? 🤔 Ведь ограничительные мероприятия в России, а в особенности в Москве, вводились сильно заранее (самоизоляция началась, когда во всей стране было менее 2000 подтверждённых случаев, в Москве — чуть более 200). Все правильно, ведь чем раньше вводятся ограничительные меры, тем они эффективнее, с экспоненциальным ростом шутки плохи. Вместе с тем, по всей видимости, используемые механизмы тестирования к этому моменту ещё не могли адекватно отображать картину происходящего. Наращивание мощностей для тестирования надо было начинать ещё в феврале/марте, на фоне событий в Европе. В Москве же только с 27 марта тестированием на коронавирус начинают охватывать родственников тех жителей, которых госпитализировали с подозрением на пневмонию. Что уж говорить о массовом выялении заболевших на ранних стадиях заболевания.
В случае Германии, где все мероприятия вводились не настолько превентивно (карантин начался, когда количество подтверждённых случаев в стране приблизилось к 30 тысячам, а в Баварии — главном очаге распространения инфекции — к 4000), тестирование, видимо, адекватно отображало текущую ситуацию. В результате, уже после двух недель карантина наблюдалась устойчивая тенденция на снижение новых регистрируемых случаев. Показатели заболеваемости монотонно пошли вниз, по ухабам модуля синусоиды, лаборатории работали штатно, без авралов, сбавляя интенсивность тестирования по выходным. Москва, где число заболевших сравнимо с таковым во всей Германии, не может похвастаться такой стабильностью, один аврал (резкое увеличение объёмов тестирования) тут явно был в начале мая (см. графики выше 📈).
Ещё один локальный выброс наблюдался в районе 19 апреля, он по всей видимости был обусловлен массовым тестированием работников городских служб (17.5 тысяч человек). К этому же времени ещё 12 частных лабораторий начали не только проводить тестирование анализов, которые были взяты сотрудниками городских медицинских организаций, но и осуществлять забор биоматериала у частных лиц самостоятельно, а также проводить исследования на коммерческой основе. Эти лаборатории, как заявлялось, могли обрабатывать сверх городских мощностей до 10 тысяч тестов в сутки, что существенно увеличило скрининговые возможности в Москве.
Главная аномалия московского графика новых регистрируемых случаев (как, впрочем, и российского) наблюдается с 30 апреля по 2 мая. В эти дни темп прироста новых больных был максимальным. Непродолжительным гуглением удалось найти причину. Всё дело в том, что с 30 апреля выявляемость коронавирусной инфекции в Москве стала «в разы лучше». Также к этому времени были перепроверены пробы тяжелобольных людей. До 50% тяжелобольных COVID-19, попавших в том числе в реанимацию, получили по две отрицательных пробы на коронавирус, заявил в эфире «России 24» мэр Москвы Сергей Собянин. Он отметил, что в отношении этих пациентов было видно, что они тяжело больны и «это точно коронавирус». Также в своём блоге мэр отметил, что в целом количество лабораторных тестов а апреле выросло в 5 раз по сравнению с мартом, а с 30 апреля стало возможным проведение до 40 тыс. ПЦР-исследований в сутки.
Вопрос о качестве используемых для диагностики тест-систем обсуждался неоднократно, с некоторыми из них действительно было много проблем. В результате лаборатории, включившиеся в тестирование населения на новую коронавирусную инфекцию, задерживали выдачу результатов. Вместо заявленных на сайтах компаний сроков исследования от одного до двух дней ожидание иногда растягивалось на неделю. Эксперты объясняли ситуацию частыми повторными верификациями проб из-за низкой чувствительности используемых тест-систем.
Напомним, что в Москве человека считают COVID-положительным уже после первого положительного анализа (изолируют). Такие анализы проходят повторное исследование в референс-центрах для подтверждения диагноза и только потом положительные результаты пападают в статистику. Поэтому медианное значение времени задержки $D$ между фактическим инфицированием человека и его попаданием в официальную статистику заболевших порядка двух недель, полученное нашей моделью, вполне согласуется с представленной выше информацией о специфике тестирования в Москве (в Германии медианная оценка $D$ для всей страны составляет около 11 дней). Дополнительный вклад в увеличение параметра $D$ в нашем случае также может вносить относительно большое время, в течение которого, заражённый уже терпит симптомы и лечится самостоятельно. Всё-таки у русского человека склонность к терпению/самолечению есть. Но суммарная величина этого вклада вряд ли больше, чем величина такового, обусловленного особенностями системы тестирования.
Можно, конечно, предположить, что если бы скрининговые мощности, на которые Москва вышла к концу апреля, были таковыми ещё месяцем ранее, то сидеть на самоизоляции пришлось бы меньше, и маски 😷 с перчатками в догонку к целому скопу ограничительных мер вводить бы не пришлось. Но, видимо, у нас, действительно, «свой путь» развития эпидемии.