Экспресс-курс диванной эпидемиологии: простейшие модели, преодоление пика и выход на плато, прогнозы на денёк.

По понятным причинам в последнее время заметно подскочил интерес буквально ко всему в интернете, причина проста – все сидят по домам. Новостные ленты сейчас, наверное, мало кто читает, слишком они стали однообразные. Даже дудлы Гугла уже начинают надоедать своим неизменным призывом stayhome. Но, если вдруг кого-то угораздит случайно ввести в строке поиска букву К, то цифры, карты распространения и прогнозы по текущей пандемии, вызванной 👑вирусом SARS-CoV-2, моментально всплывут на экране и Гугл заботливо добавит на страницу поисковой выдачи локализованное, красное, тревожное оповещение. Неудивительно, что число домашних эпидемиологов и специалистов по статистике значительно увеличилось, карантинное самообразование – великая вещь. Мы тоже примкнем к этой толпе диванных аналитиков, но рассмотрим лишь основные принципы построения простейших эпидемиологических моделей и получения с их помощью некоторых прогнозов на перспективу. Здесь сразу необходимо подчеркнуть, что сильно впечатляться этими прогнозами не следует, задача статьи лишь познакомить читателя с базовыми принципами их получения.

Ваше купе, Сир

Если верить Википедии, то основу эпидемиологического моделирования составляют так называемые компартментальные модели. Они используются для упрощения математического моделирования инфекционных заболеваний. Население при этом делится на некоторые группы (compartiment в переводе с французского означает отсек, отдельная емкость, бункер, купе) и подразумевается, что каждый человек в одной и той же группе имеет одинаковые показатели.

Компартментальные модели, как правило, исследуются с помощью систем обыкновенных дифференциальных уравнений (детерминированных), но их также можно рассматривать и в стохастической структуре, которая является более реалистичной, но и более сложной для анализа. Лучшее видео, наглядно демонстрирующее всю суть таких моделей и симуляцию различных сценариев с их использованием, вышло в конце марта на канале 3Blue1Brown. Объяснить доступнее вряд ли у кого-то получится, в общем рекоммендед.

Компартментальные модели могут использоваться для прогнозирования свойств распространения некоторого заболевания, таких например, как распространенность заболевания или продолжительность соответствующей эпидемии. Кроме того, компартментальные модели позволяют понять, как различные факторы, будь то закрытие общественных мест, улучшение гигиены или карантин самоизоляция, могут влиять на ход эпидемии.

Одной из простейших компартментальных моделей является модель SIR. Многие более сложные эпидемиологические модели строятся уже на её основе. Согласно модели SIR индивиды делятся на три группы: S (susceptible) – восприимчивые к заболеванию, I (infectious) – инфицированные и R (recovered) – выздоровевшие. Название последней группы иногда указывают как removed, и это лучше отражает её суть, поскольку в эту группу в такой простой модели входят не только выздоровевшие, но и все индивиды, которые переболели, умершие (deceased) в том числе. Иначе говоря, последняя группа R removed = recovered + deceased – это переболевшие.

Так как зачастую динамика эпидемии, например того же гриппа, намного быстрее, чем динамика рождения и смерти в популяции, в простых компартментальных моделях показатели рождаемости и смертности не учитываются. В рамках рассматриваемой модели это тоже так, поскольку смертность от болезни в популяции не учитывается явно. Выздоровевшие и умершие формируют общую группу переболевших индивидов.

Модель SIR обладает достаточной предсказательной силой для инфекционных заболеваний, которые передаются от человека к человеку, и где выздоровление обеспечивает относительно длительную резистентность. Допустим, опять же для простоты, что COVID-19 является таким заболеванием.

Переменные $S$, $I$ и $R$ представляют количество людей в каждой группе в конкретное время $t$, т.е. количество людей в каждой группе рассчитывается в соответсвии с функциями времени: $S(t)$, $I(t)$ и $R(t)$. Модель SIR в таком случае представляет собой нелинейную систему дифференциальных уравнений (ДУ), описывающих динамику распространения заболевания в популяции:

Здесь $S(t)$ — численность восприимчивых индивидов в момент времени $t$; $I(t)$ — численность инфицированных индивидов в момент времени $t$; $R(t)$ — численность переболевших индивидов в момент времени $t$; $N$ — численность популяции; $\beta$ — коэффициент интенсивности контактов индивидов с последующим инфицированием; $\gamma$ — коэффициент интенсивности перехода инфицированных индивидов в группу переболевших.

В англоязычной литературе параметр $\beta>0$ называется эффективной частотой контактов (effective contact rate). Вычисляется этот показатель как среднее количество контактов между инфицированным и восприимчивыми индивидами в день $\bar{c}$, умноженное на вероятность передачи заболевания $\tau$ (transmissibility) при контакте инфицированного индивида с неинфицированным $\beta=\bar{c}\tau$. В простейшей модели SIR обычно предполагается, что эта вероятность равна единице, т.е. при контакте здорового индивида с инфицированным заражение первого неизбежно. Параметр $\beta$ в таком случае характеризует интенсивность контактов индивидов с последующим инфицированием. Тогда $\beta{IS/N}$ — это прирост инфицированных (rate of new infections). Эффективная частота контактов $\beta$ (среднее число контактов между инфицированным и неинфицированными индивидами в день, при которых происходит передача заболевания, т.е. скольких восприимчивых индивидов в день в среднем заражает один инфицированный) делится на размер популяции $N$, в итоге получается средняя доля популяции $0<\beta{/N}<1$, заражаемая одним инфицированным в день, — вероятность заражения при контакте восприимчивого индивида с произвольным индивидом из популяции (infection rate, все индивиды распределены в популяции равномерно и каждая пара индивидов имеет равную вероятность вступить в контакт друг с другом), которая затем умножается на число всех возможных контактов (пар) между восприимчивыми и инфицированными индивидами в популяции в текущий день $SI$, всё логично.

Таким образом, первое уравнение в системе означает, что изменение числа здоровых, восприимчивых к заболеванию индивидов уменьшается со временем пропорционально числу контактов с инфицированными $-\beta{IS/N}$. После контакта происходит заражение, восприимчивый переходит в состояние инфицированного. Второе уравнение показывает, что скорость увеличения числа заразившихся растет пропорционально числу контактов здоровых и инфицированных $\beta{IS/N}$ и уменьшается по мере выздоровления последних $-\gamma{I}$, третье уравнение – что число переболевших в единицу времени пропорционально числу инфицированных $\gamma{I}$.

Параметр $0<\gamma<1$ характеризует интенсивность перехода инфицированных индивидов в группу переболевших (removed) или интенсивность выбывания индивидов (removal rate), т.е. показывает какая доля от текущего числа инфицированных переходит в состояние переболевших.

Распространение заболевания в модели SIR происходит по незатейливой схеме “восприимчивые становятся инфицированными, потом переходят в разряд переболевших”:

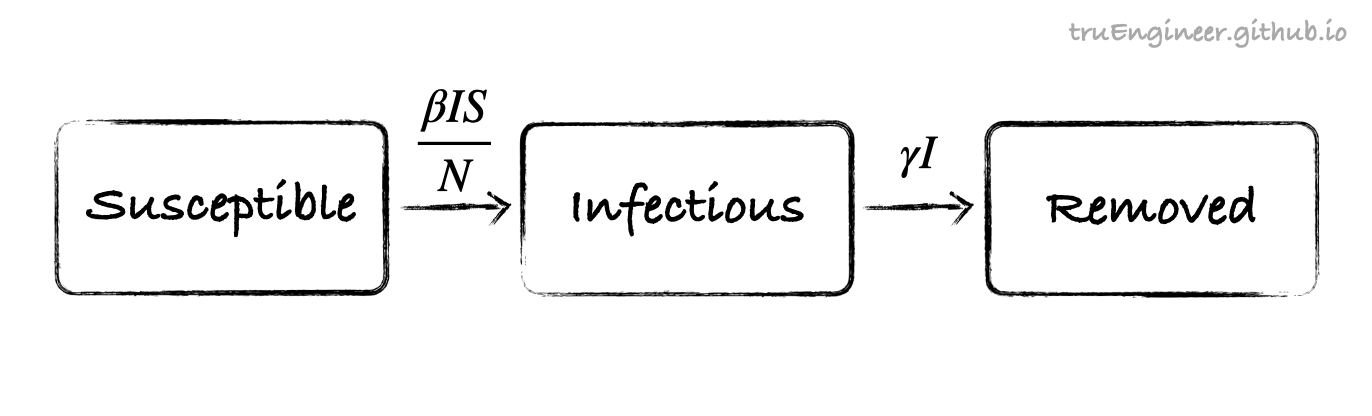
Стрелки на схеме выше помечены скоростями перехода индивидов между группами.

Коэффициенты $\gamma$ и $\beta$ также могут быть выражены соответственно через среднее время между контактами $T_c$ и среднее время, за которое болезнь заканчивается с тем или иным исходом $T_r$. Здесь необходимо отметить, что за время $T_r$ инфицированный может заражать других, поэтому $T_r$ ещё иногда называют средним временем заразности (mean infectious time):

Если сложить все три уравнения приведённой выше системы ДУ SIR, то получим, что:

Т.е. численность популяции – это некоторая константа $N$, которая не меняется в течение эпидемии:

Решать такую систему ДУ на практике чаще всего приходится численно, хотя для простейших случаев, вроде рассматриваемого тут, это можно сделать и аналитически. Решать ДУБы🌳 (дифференциальные уравнения Бернулли) умеет любой инженер.

Вместо аналитического решения системы ДУ ограничимся рассмотрением пары занимательных фактов. Второе уравнение системы можно переписать в виде:

Параметр $R_0$ здесь вычисляется как:

Это так называемое базовое репродуктивное число (Basic reproduction number) – среднее ожидаемое количество вторичных случаев заражения, вызванное одним зараженным человеком в полностью восприимчивой популяции (которая никогда раньше не сталкивалась с этой болезнью), т.е. скольких человек в среднем заражает один больной.

Из представленного выше уравнения для $I’(t)$ следует, что количество одномоментно болеющих человек $I$ (инфицированных), определяется в модели SIR параметром $R_0$. Так, при $R_0>N/S(0)$, где $S(0)$ – это первоначальный размер восприимчивой к патогену популяции ($S(0)\leq{N}$), значение производной $I’(0)>0$, а значит произойдет вспышка заболевания с последовательным увеличением числа заражённых $I$ во времени, которая потенциально сможет охватить значительную часть населения. Если же $R_0<N/S(0)$, тогда производная $I’(0)<0$, и независимо от первоначального размера восприимчивой популяции $S(0)$ заболевание не может вызвать эпидемическую вспышку. Вот почему значение $R_0$ важно для эпидемиологов. Если считать восприимчивой всю популяцию ($S(0)=N$), то при $R_0$ большем 1 инфекция, скорее всего, будет продолжать своё распространение в популяции, а если меньше 1, то вспышка, скорее всего, прекратится. Базовое репродуктивное число не является неким неизменным свойством самого патогена. В местах с хорошим инфекционным контролем, где заболевших быстро изолируют, его оцениваемое значение обычно более низкое, чем в местах, где первоначально происходит вспышка. $R_0$ – это мера потенциала распространения болезни в популяции, а уменьшить это число помогают меры противодействия распространению инфекции.

Для большинства эпидемий прошлых лет и разного рода сезонных эпидемий соответствующие показатели $R_0$ оценены. Так, для эпидемий сезонного гриппа это число в среднем составляет 1.5, у пандемии испанского гриппа образца 1918 года оно составляло 2.1. Округлив $R_0$ испанки до 2 можно примерно представить, что распространялся этот вирус как-то так:

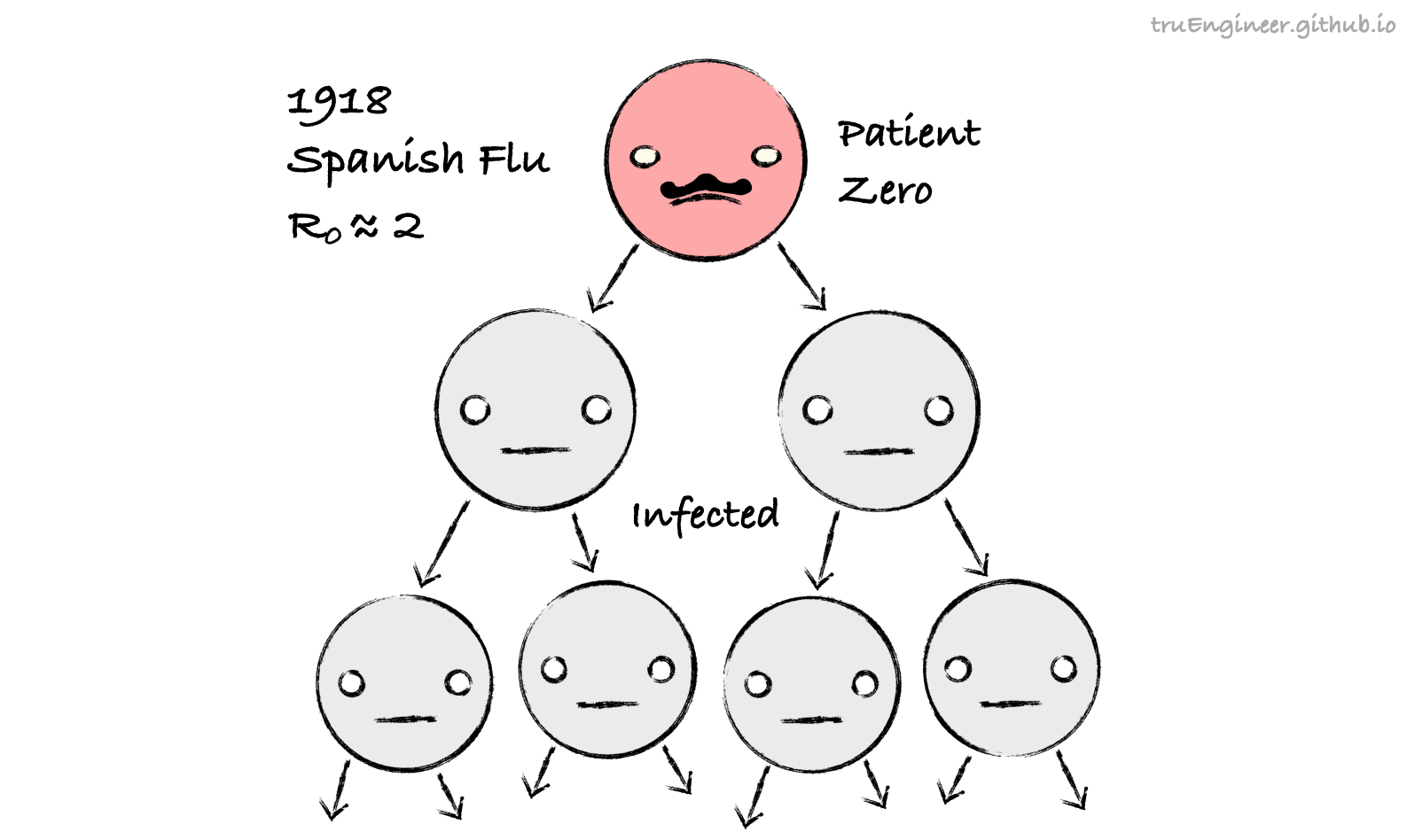
Объявившийся в Южном Китае в начале 2000-х годов вирус SARS-CoV-1, дальний родственник нынешнего, также вызывал тяжелый острый респираторный синдром (ТОРС, SARS). По имеющимся оценкам базовое репродуктивное число для него составляло значение около 4, т.е. потенциал для распространения у него был больше, чем у гриппа:

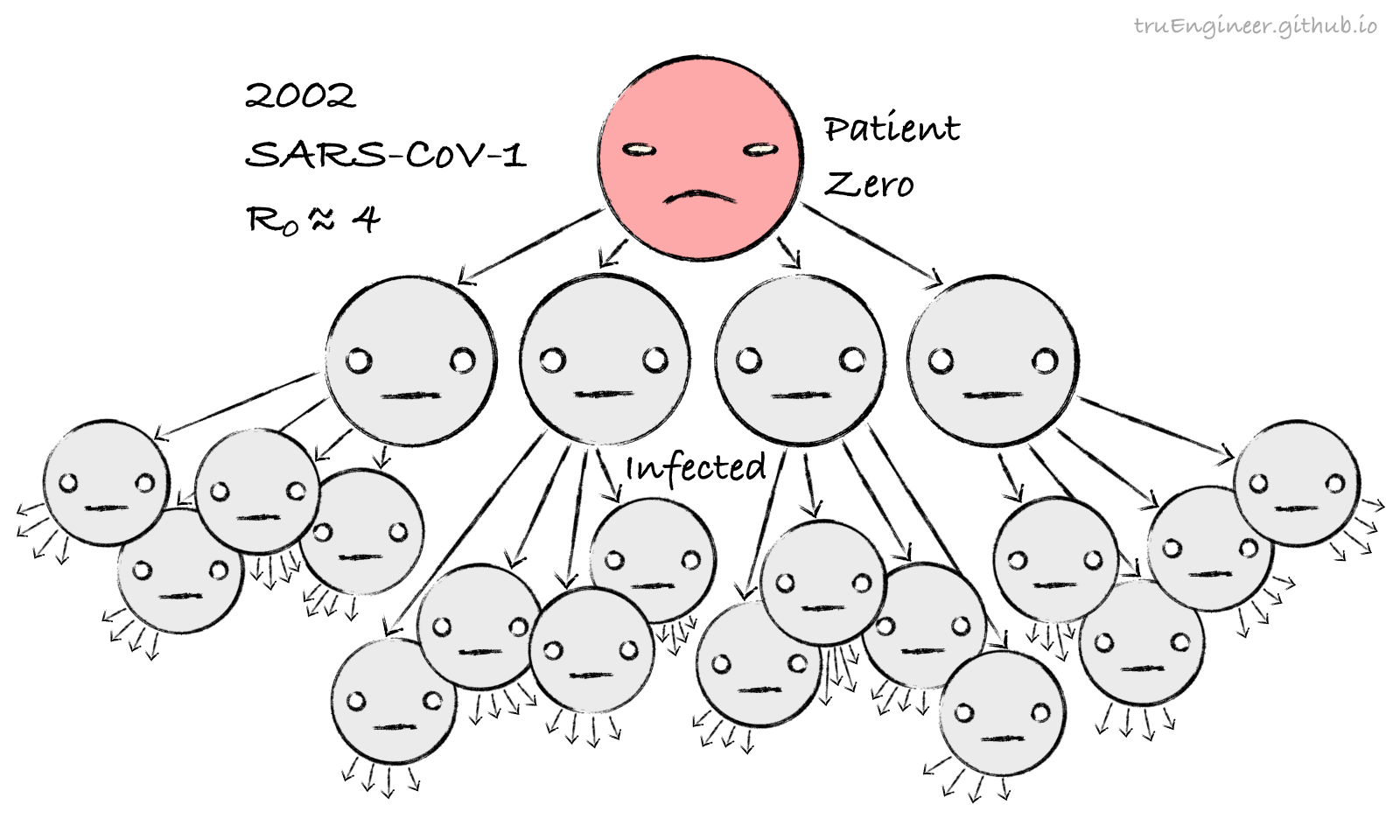
На первый взгляд SARS-CoV-1 выглядит страшнее. Но большее значение $R_0$ не обязательно означает более худший сценарий. Сезонный грипп имеет $R_0$ около 1.5, и им заражаются миллионы людей каждый год. SARS с $R_0=4$ был выявлен у чуть более, чем у 8000 человек. Испанский же грипп с $R_0=2$ охватил до 30% населения Земли того времени, а количество жертв этой пандемии исчислялось десятками миллионов.

Что касается новичка коронавируса SARS-CoV-2, то $R_0$ для вызываемого им COVID-19 оценивается в диапазоне от 2.24 до 3.58. Есть и более пессимистические оценки, со значениями порядка 6.4. В любом случае, как мы уже убедились, этого достаточно, чтобы поддерживать огонь пандемии.

Маленькая школьная эпидемия

Рассмотрим модель SIR на конкретном примере. Допустим, что в некоторой организации, пусть это будет школа, в которой работают/учатся 2000 человек, появился мистер-икс, который накануне поел супчик из летучей мыши прилетел из одной далёкой страны. Вместе с багажом впечатлений о своей поездке он привез некий экзотический штамм вируса, к которому восприимчивы абсолютно все без исключения. Он и стал нулевым пациентом.

Параметры модели будут следующими: размер популяции $N=2\cdot10^3$, один инфицированный в начале эпидемии (нулевой пациент), среднее число контактов с последующим инфицированием на одного человека в день $\beta=1.5$ (инфицированный может заразить трех восприимчивых за два дня, среднее время между контактами $T_c=0.66$), интенсивность выбывания индивидов $\gamma=0.5$ (инфицированный может заражать других в течение двух дней $T_r=2$). Соответственно, базовое репродуктивное число $R_0={\beta}/{\gamma}=3$.

Решать систему дифференциальных уравнений SIR будем численно, используя связку библиотек NumPy+SciPy. Соответствующий IPython-ноутбук с реализацией этого численного решения находится в репозитории. Там можно осуществить расчёт и для других параметров модели. Здесь же представлены графики развития эпидемии согласно модели SIR с параметрами, представленными ранее:

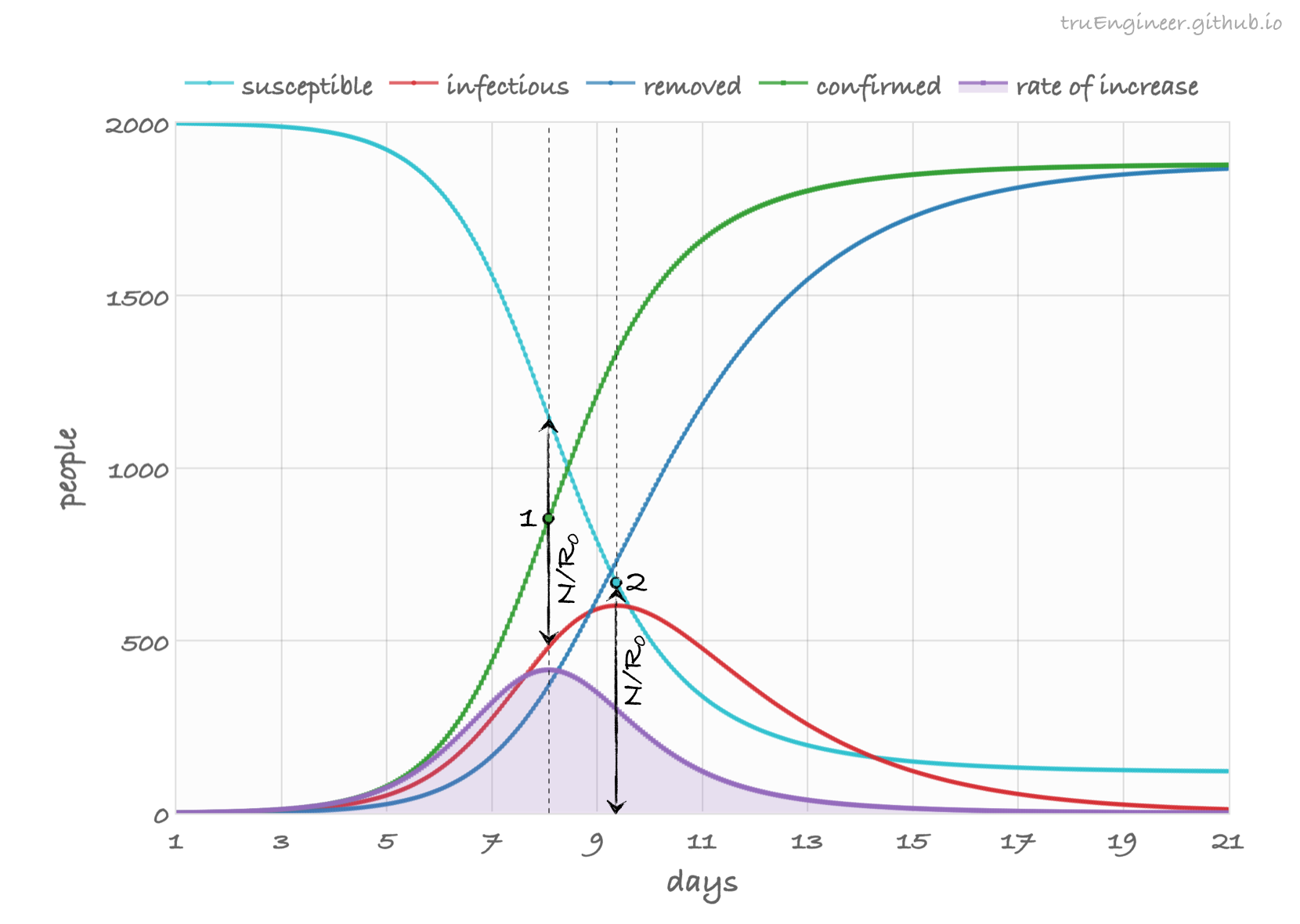
Как видим, переболели почти все. Помимо графиков текущего числа восприимчивых (susceptible), зараженных (infectious), и переболевших (removed), здесь приведен график роста общего числа подтверждённых случаев заболевания (confirmed cases), представляющий собой в модели SIR сумму текущего количества болеющих и переболевших (confirmed cases = infectious + removed). Именно эту кривую регулярно демонстрирует ВОЗ, различные сайты типа worldometer и тревожные стримы на YouTube. Также здесь приведен график производной подтвержденных случаев, характеризующий темп их роста (rate of increase). График переболевших, как уже упоминалось ранее, включает в себя как выздоровевших (recovered), так и умерших (deceased):

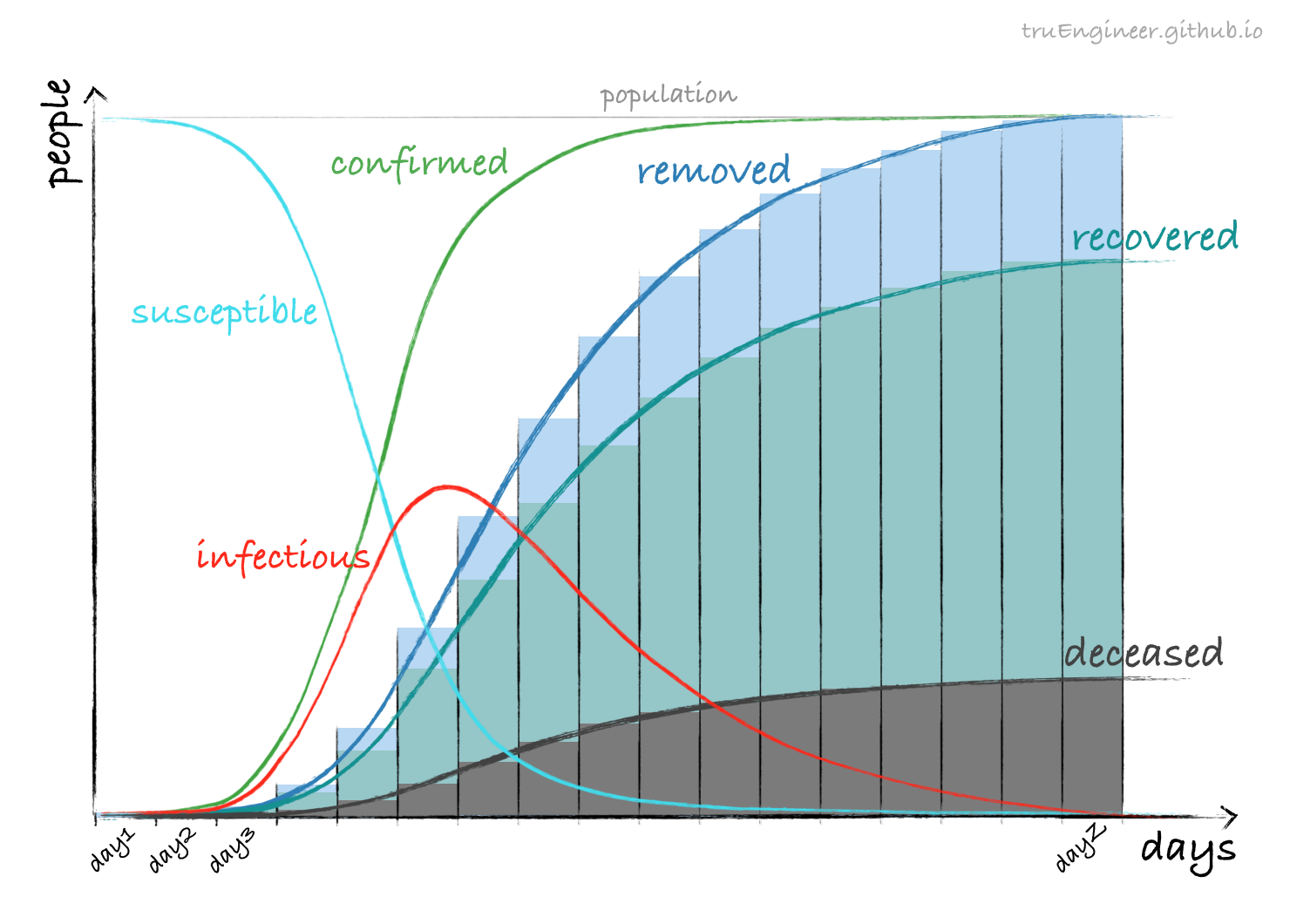
Что же такое пик эпидемии? На приведенном выше графике SIR-модели для школьной эпидемии мы можем наблюдать две точки. Именно о них так или иначе говорят журналисты, то и дело путая их между собой. Первая точка – точка перегиба (inflection point) кривой подтвержденных случаев. Скорость прироста подтвержденных случаев в этой точке максимальна, график соответствующей производной достигает своего пика – пика темпа роста подтвержденных случаев (rate of increase):

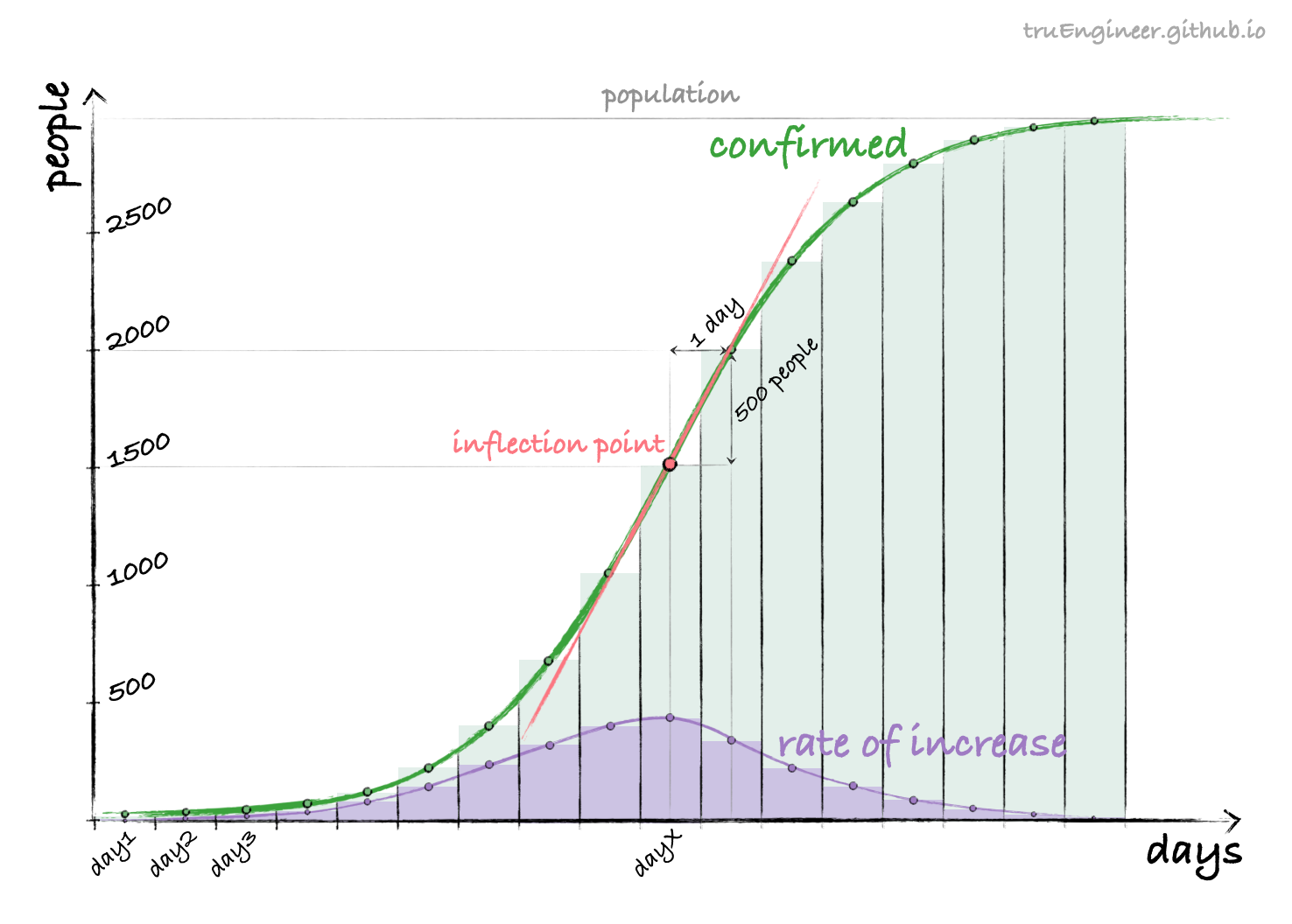
Это первый стресс-тест системы здравоохранения. Количество новых зарегистрированных случаев заболевания в этот день будет максимальным, следовательно больных, которых необходимо госпитализировать, тоже будет больше обычного, и всем из них должно хватить мест.

Для того, чтобы определить день, когда эта точка будет пройдена, необходимо вспомнить тот факт, что в точке перегиба вторая производная функции $C(t)=I(t)+R(t)$, описывающей текущее число подтверждённых случаев, должна быть равна нулю. Т.е. необходимо продифференцировать сумму второго и третьего уравнений (для $I$ и $R$) приведённой выше системы ДУ SIR, приравнять полученную вторую производную $C^{″}(t)$ к нулю и решить это уравнение относительно $t$:

Таким образом, пик темпа роста подтвержденных случаев (rate of increase) достигается, когда разность текущего количества восприимчивых и инфицированных индивидов составляет величину $N/R_0$.

Вторая точка – максимум зараженных на данных момент людей, или пик текущего числа болеющих, определяется проще. Для этого необходимо приравнять к нулю производную $I’(t)$, т.е. второе уравнение системы ДУ SIR:

Здесь также, как и в предыдущем случае, фигурирует величина $N/R_0$. Магия числа $R_0$ в модели SIR присутствует везде.✨

Итак, если первый пик был пройден успешно, а карантинные мероприятия эффективны, то система здравоохранения должна справиться с нагрузкой и при прохождении второго. Ну а что касается “плато”, то это понятие, как и “пик эпидемии” сильно зависит от контекста. На графиках школьной эпидемии их аж целых четыре. Первое плато расположено в районе максимума темпа роста подтверждённых случаев (фиолетового графика). Во время его прохождения количество ежедневно регистрируемых случаев практически не меняется, а потом идёт на спад. Второе плато – плато текущего числа болеющих (красный график), после прохождения которого, мы через некоторое время переходим на плато подтверждённых случаев (зелёный график), и, наконец, ближе к концу эпидемии, мы оказываемся на плато переболевших. Сюжет развивается как в фэнтези.🦄

Подгонка под данные и магия предсказаний

Настало время применить полученные знания на практике. Объектом нашего интереса, разумеется, будет COVID-19. Он вообще будет всем интересен до конца этого года уж точно. Возьмём набор данных университета Джонса Хопкинса, в котором содержится информация о текущем количестве подтвержденных случаев заболевания COVID-19 по всем странам, начиная с 22 января 2020 года, но ограничимся рассмотрением этого показателя только в США, популярном нынче объекте для исследований в этом контексте. Рассматриваемые далее модели доступны в том же репозитории.

Для начала попытаемся аппроксимировать данные по количеству подтверждённых случаев в США, используя модель SIR. Для этого будем численно решать соответствующую систему ДУ integrate.odeint, а затем аппроксимировать полученное решение некоторой кривой optimize.curve_fit, на основе которой в перспективе будем делать прогнозы.

Итак, задача модели sir_model_2p (2pSIR на графиках) состоит в определении параметров $\beta$ (beta) и $\gamma$ (gamma). В качестве размера популяции, параметра $N$ модели, возьмём население США по оценке на 2019 год $N_{US}=328.2\cdot10^6$. А числа восприимчивых, зараженных и инфицированных в начале эпидемии (начальные условия модели) пусть будут следующие: $S(0)=N_{US}-1$, $I(0)=1$, $R(0)=0$. Первая функция sir_model_2p модели задаёт систему ДУ SIR, рассмотренную ранее. Задача второй функции fit_odeint_2p – численное решение этой системы (integrate.odeint) и возврат суммы интегралов, соответствующих количеству заражённых и переболевших – подтверждённых случаев заболевания (confirmed cases) на каждый день в векторе времени t. Подгонка полученных значений суммы интегралов к данным y_data, с соответствующим временем измерений t_data, и вычисление оценок неизвестных параметров popt (popt[0] для $\beta$, popt[1] для $\gamma$) производится с помощью функции optimize.curve_fit, путём минимизации суммы квадратов отклонений между данными и получаемыми от fit_odeint_2p значениями. Так как для параметров здесь указываются границы bounds, то, согласно документации, при поиске этих параметров используется численный метод оптимизации trf (Trust Region Reflective), базирующийся на определении региона вокруг лучшего решения, в котором квадратичная модель аппроксимирует целевую функцию.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
Nus = 328.2e6 # 2019 US population

# SIR model ODE system
def sir_model_2p(y, t, beta, gamma): # 2 unknown parameters
    S, I, R = y # y[0]: susceptible, y[1]: infectious, y[2]: removed 
    dSdt = -beta * S * I / Nus
    dIdt =  beta * S * I / Nus - gamma * I
    dRdt =  gamma * I
    return dSdt, dIdt, dRdt

# Integrate a system of ODEs
def fit_odeint_2p(t, beta, gamma):
    # initial conditions (S(0)=Nus-1, I(0)=1, R(0)=0)
    ints = integrate.odeint(sir_model_2p, (Nus-1.0, 1.0, 0.0), t, args=(beta, gamma))
    return ints[:,1] + ints[:,2] # [:,1]: infectious + [:,2]: removed = confirmed cases

popt, pcov = optimize.curve_fit(fit_odeint_2p, t_data, y_data, bounds=([0,0], [np.inf,1]))
y_fitted = fit_odeint_2p(t_data, *popt)

Для начала посмотрим как эта модель аппроксимирует данные по состоянию на 25 апреля при различных значениях размеров популяции $N_{US}$, в которой распространяется патоген, и различных подходах к получению оценок размера популяции $\hat{N}_{US}$:

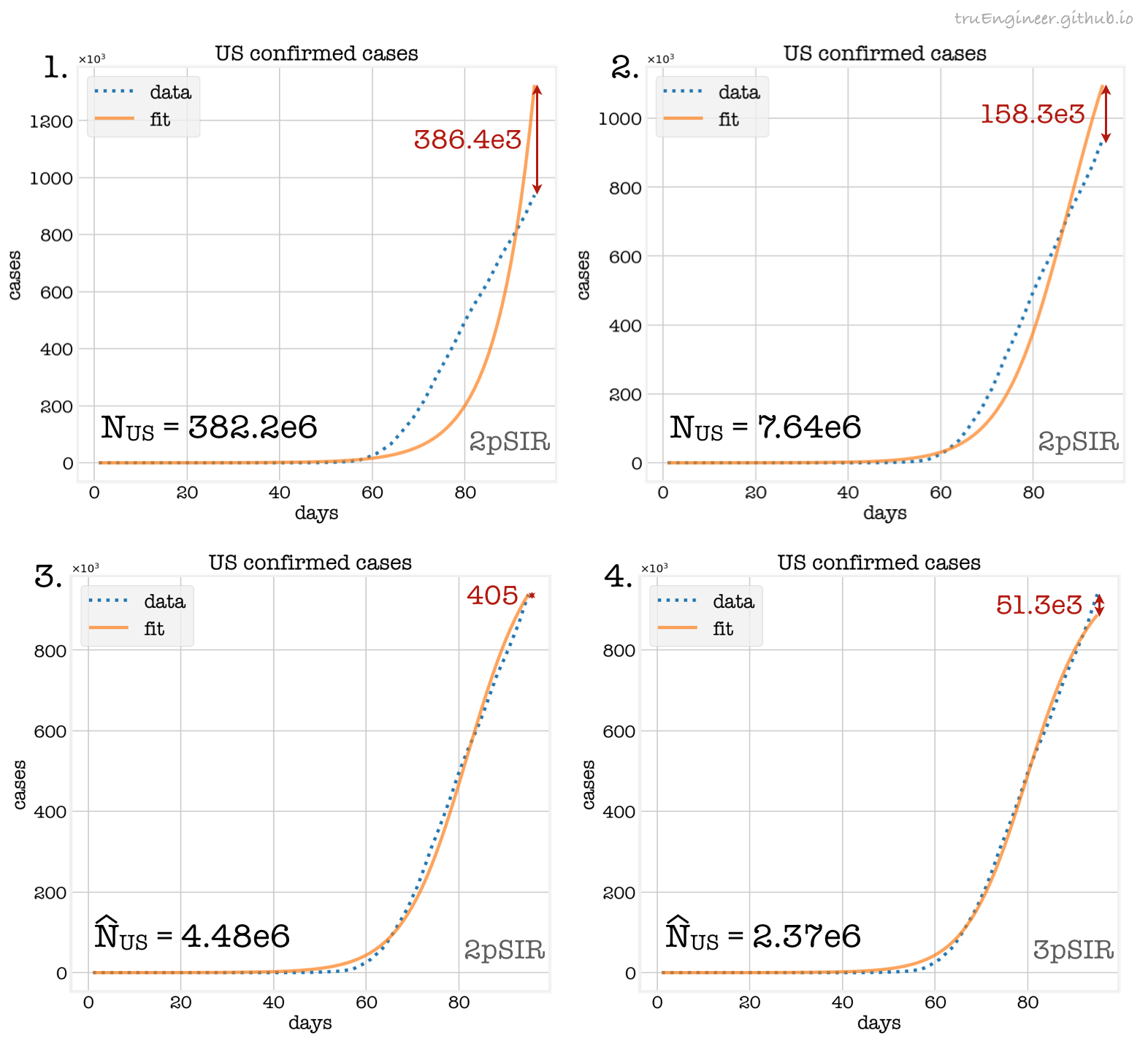
На первом графике ошибка аппроксимации в последний день максимальная. Размер популяции $N_{US}=328.2\cdot10^6$, использованный в модели, очевидно, слишком велик. Уменьшение $N_{US}$ до двух процентов населения США $7.64\cdot10^6$, а соответственно и уменьшение восприимчивой популяции при инициализации модели $S(0)=N_{US}-1$ (там ведь, всё-таки, карантин), демонстрирует правильность этого предположения. Ошибка аппроксимации на втором графике уже значительно меньше.

Можно также попробовать перебрать все возможные значения размера популяции в модели (классический bruteforce), минимизируя ошибку в последний день. Это долго, зато позволяет получить оценку $\hat{N}_{US}=4.48\cdot10^6$ (шаг, использовавшийся при переборе, составлял $10^4$), ошибка в последний день при этом падает до 405 случаев (можно уменьшить эту величину, уменьшив шаг перебора). Сделать подбор $N_{US}$ более эффективным можно, написав новую модель sir_model_3p (3pSIR на графиках), с тремя неизвестными параметрами, одним из которых будет являться размер популяции $N_{US}$ (pop), но определяется он теперь путём минимизации суммы квадратов ошибок по всем имеющимся данным.

1
2
3
4
5
6
7
8
9
10
11
12
13
def sir_model_3p(y, t, beta, gamma, pop): # 3 unknown parameters
    S, I, R = y 
    dSdt = -beta * S * I / pop
    dIdt =  beta * S * I / pop - gamma * I
    dRdt =  gamma * I
    return dSdt, dIdt, dRdt

def fit_odeint_3p(t, beta, gamma, pop):
    ints = integrate.odeint(sir_model_3p, (pop-1.0, 1.0, 0.0), t, args=(beta, gamma, pop))
    return ints[:,1] + ints[:,2]

popt, pcov = optimize.curve_fit(fit_odeint_3p, t_data, y_data, bounds=([0,0,y_data[-1]], [np.inf,1,Nus]))
y_fitted = fit_odeint_3p(t_data, *popt)

Работает эта модель гораздо быстрее чем 2pSIR с брутфорсом. Результат её работы представлен на четвёртом графике. Полученная в этом случае оценка параметра pop составила величину $\hat{N}_{US}=2.37\cdot10^6$. Так как оптимизация велась по всем данным, то и ошибка аппроксимации в последний день тут довольно большая, по сравнению с брутфорсом по этому дню (третий график), ничего удивительного, зато в предыдущие дни ошибки меньше.

Аппроксимация – это, конечно, хорошо, но задача моделей – делать прогнозы. Давать долгосрочные прогнозы с такими простыми моделями мы не возьмёмся, вместо этого будем делать прогнозы на один день, следующий за текущим последним днём в наборе данных. Сценарий будет такой: каждый день мы загружаем данные из репозитория университета Джонса-Хопкинса, обучаем на них модель и делаем прогноз на следующий день по количеству подтвержденных случаев. Почти как прогноз погоды.⛅ Проверим теперь эти модели в рамках описанного сценария.

На примере модели 2pSIR рассмотрим, как с её помощью сделать прогноз на следующий день. Всё, что необходимо сделать, после получения параметров popt, описывающих имеющиеся данные – вычислить с их помощью значение суммы интегралов заражённых и переболевших для нового, увеличенного на день вектора времени t_data+[t_data[-1]+1]. В последнем элементе массива fitprednd[-1] и будет содержаться прогноз на следующий день. Вот и вся магия. 🧙🏼‍♂️

1
2
popt, pcov = optimize.curve_fit(fit_odeint_2p, t_data, y_data, bounds=([0,0], [np.inf,1]))
fitprednd = fit_odeint_2p(t_data+[t_data[-1]+1], *popt) # next day prediction

На представленных ниже графиках зелёным цветом показаны огибающие каждодневных прогнозов на следующий день, полученные моделью 2pSIR:

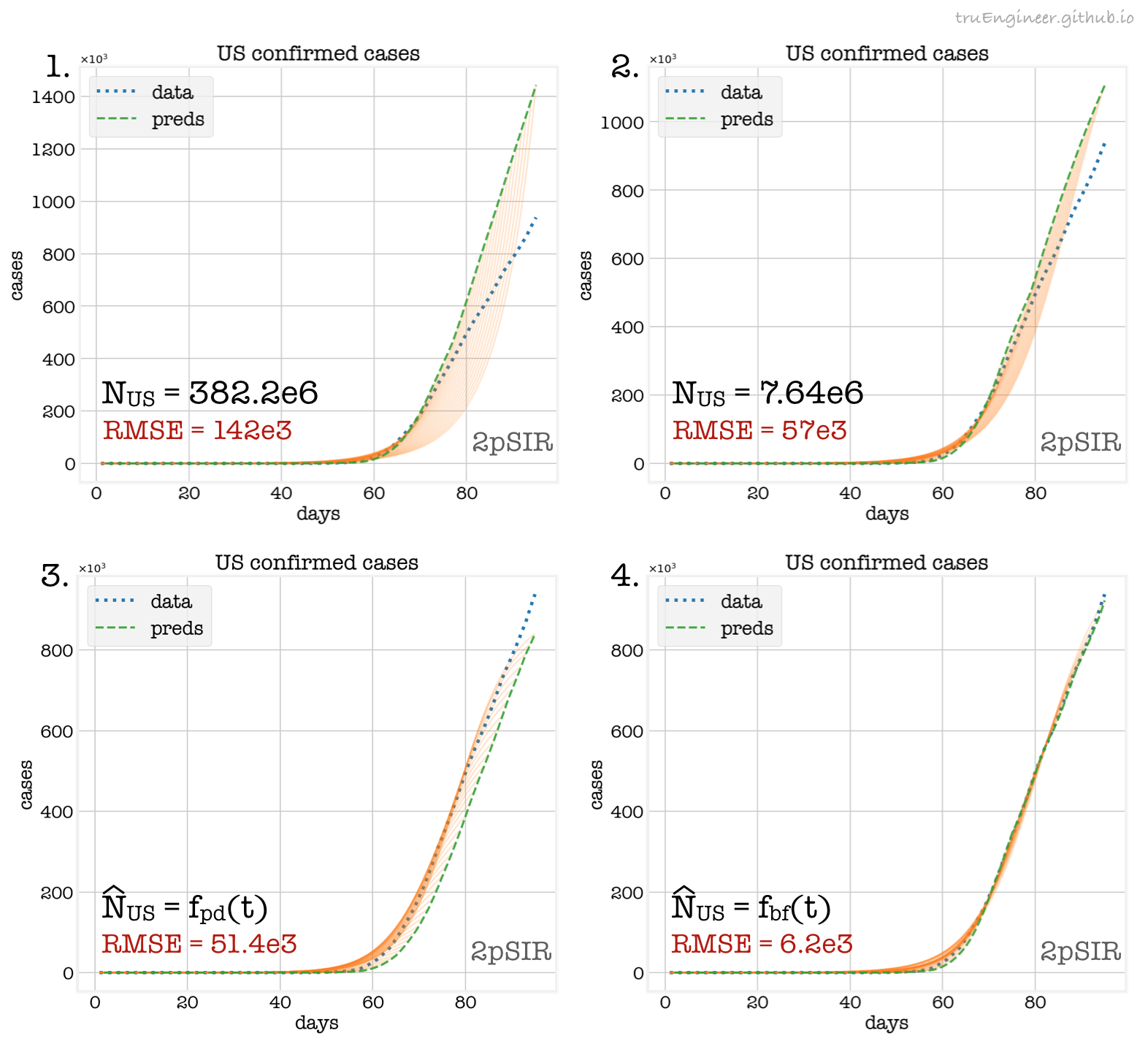
Как и в случае рассмотренной ранее аппроксимации, особенно сильное влияние на прогнозы оказывает размер популяции, в которой распространяется заболевание. На первом и втором графиках представлены прогнозы для фиксированных значений $N_{US}$, тенденция на более высокую точность при меньшем размере популяции сохранилась. На третьем графике представлен случай, когда в качестве размера популяции при расчёте прогноза на следующий день бралось текущее количество подтверждённых случаев в день предшествующий ему, т.е. оценка $\hat{N}_{US}$, бралась из данных $f_{pd}(t)$ (previous day), разумеется точность в этом случае тоже далека от идеала, ведь слишком занижен размер восприимчивой популяции. Наконец, на четвёртом графике, оценки $\hat{N}_{US}$ при обучении модели получались старым, добрым брутфорсом $f_{bf}(t)$ (bruteforce), минимизируя ошибку на текущий день в наборе данных, чтобы потом сделать прогноз на следующий. Это самый долгий и самый точный способ среди рассмотренных тут случаев. Соответствующие значения корня из среднеквадратической ошибки (RMSE) между прогнозом и реальными данными приведены на всех графиках.

Прогнозы на следующий день, полученные более быстрой моделью 3pSIR, обученной на имеющихся в текущий день данных, представлены ниже:

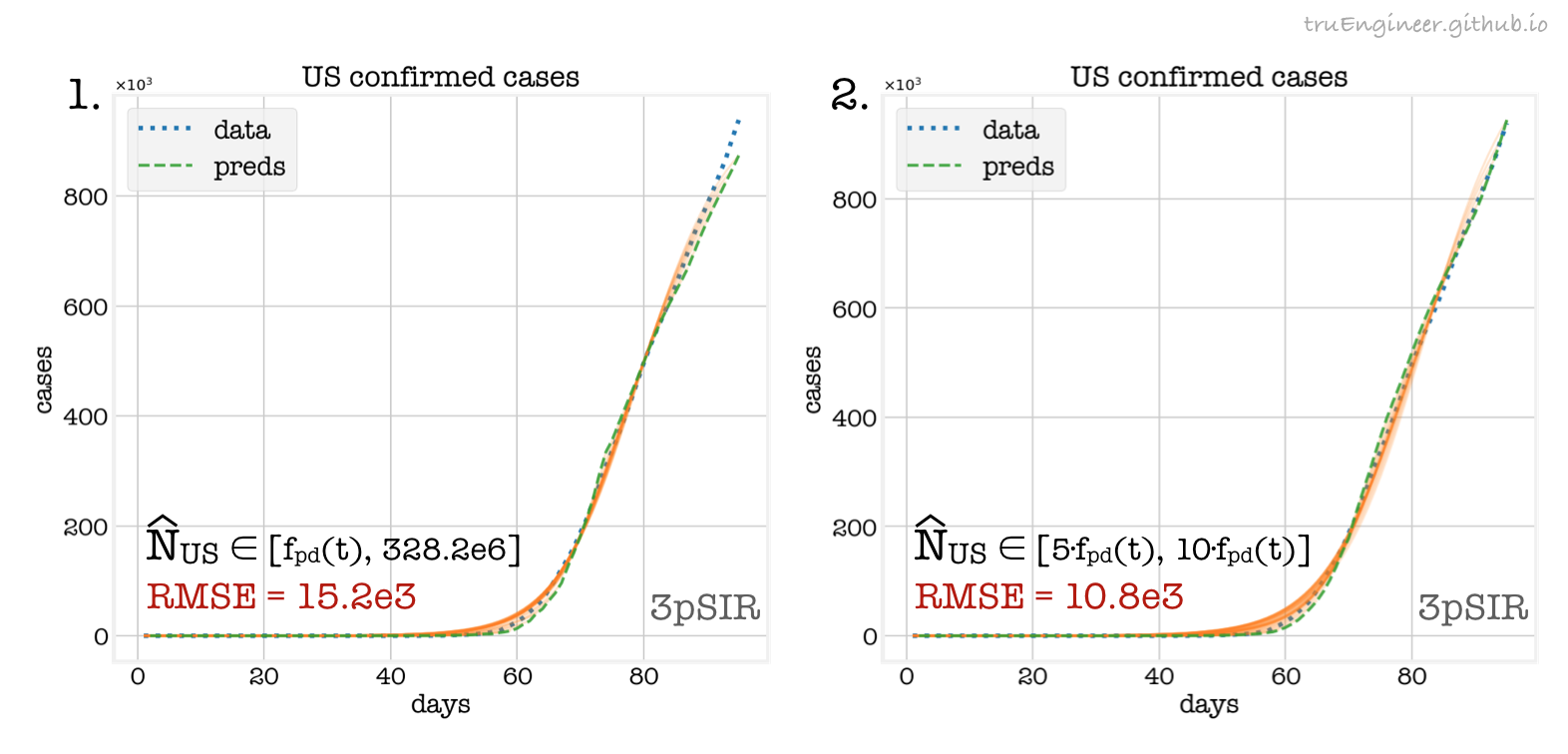
На этих графиках указаны соответствующие границы (bounds), в которых осуществлялся поиск оптимальных оценок $\hat{N}_{US}$, и значения RMSE. В качестве нижней границы использовалось число подтверждённых случаев в день, предшествующий предсказываемому, $f_{pd}(t)$. На втором графике представлена совсем уж эмпирическая стратегия, которая подразумевает установку нижней и верхней границ для $\hat{N}_{US}$ соответственно в пять и в десять раз больше, чем количество случаев в предшествующий день $f_{pd}(t)$.

Вообще говоря, оценка размера охватываемой заболеванием популяции ($N$) и, как следствие, начальных условий эпидемиологической модели ($S(0)$, $I(0)$, $R(0)$), в особенности начального числа восприимчивых индивидов $S(0)$, является отдельной нетривиальной задачей. Но и рассмотренные здесь эмпирические стратегии имеют место быть и позволяют давать прогнозы в рамках страны на один день вперёд с погрешностью в пару тысяч или даже в несколько сотен случаев, что не так уж и плохо, когда ежедневный прирост больных составляет десятки тысяч.

Конечно, это всё баловство, причиной которого явилось внезапно увеличившееся количество свободного времени, но в целом задача статьи заключалась в обзоре базовых принципов формирования простейших прогнозов. Кто-то сейчас сидит на Kaggle и обучает переобучает под эту же задачу универсальные аппроксиматоры нелинейных функций – нейронные сети, паля из пушки по воробьям.💥 Предсказательная сила таких моделей на длительную перспективу тоже не выдающаяся. Долгосрочных точных прогнозов по эпидемии не даст, пожалуй, никто, даже ведущие эксперты ВОЗ. Но заходить на их сайт периодически стоит, там бывают полезные рекомендации:

Пост получился довольно большим, пора бы уже закругляться. Сделать это надо как-то пафосно, вспомнив слова классиков. В этом случае как нельзя лучше подойдет фраза одного из авторов преобразования Бокса-Мюллера, а именно Джорджа Бокса: “В сущности, все модели неправильны, но некоторые из них полезны”. Или в оригинале: “All models are wrong, but some are useful”. Может быть и рассмотренная тут модель какой-нибудь минимальной полезностью да и обладает. ᕕ( ᐛ )ᕗ